Oscilloscope as a lock-in amplifier (Rigol DS1054Z)

[RoGeorge]

A lock-in amplifier is an instrument to measure very small AC signals flooded with noise.  A lock-in amplifier is able to clean up signals many times smaller than the noise, and measure their amplitude and phase.

To achieve that, it needs a clean reference signal that is synchronous with the small one we want to measure.  The amplitude of the reference signal is irrelevant, same for the phase, just that the reference signal must be synchronous and clean.



The typical arrangement is like this:  A generator of clean signal is feeding both the device under test and the reference input, while the small signal flooded in noise (that gets out from the device under test) is fed to the measuring input of the lock-in amplifier.  At the output we will get the phase and the amplitude of the small signal.



The trick to achieve this is that the lock-in amplifier averages many periods of the signal, so the noise will average to zero.  The signal of interest will average to zero, too, except that the averaging is made synchronous with the small signal of interest (that is why it needs a clean synchronous reference signal).  As a result, the noise averages to zero, while the signal of interest averages to itself (stays the same).

Thus, all the noise is removed while the small signal of interest remains, because the small signal was synchronous with the averaging process.

Usually this functionality is implemented with analog multipliers followed by integrator circuits, sometimes by simply switching the polarity (multiply with +1/-1) followed by integrator, sometimes is made purely digital by DSP.

We will implement a lock-in amplifier with an oscilloscope, by synchronizing the oscilloscope on the clean Vref (Ch2), while feeding the small noisy signal to Channel 1, then setting the acquisition mode on Average (between consecutive traces), on DS1054Z by pressing Acquire -> Mode -> Average.

The multiplication here is made with 0/1 (by the triggering circuit) and the integration is made by the trace averaging mode (also there is no need to get the quadrature reference signal, since the multiplication and averaging happens for each and every ADC sample, including t=0, or t=pi/2, or any other point on the trace).

As a bonus, this kind of lock-in amplifier not only gives the amplitude and phase, but also shows the waveform of the small signal, which might be a big advantage, and also can work at much higher frequencies.  As a drawback, an oscilloscope might not have such a big dynamic range as a dedicated lock-in amplifier.


As an application of this technique, let's measure the contact resistance of some random banana plugs.



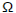
We set a 50 DDS generator to output 10Vpp at 1.3kHz and measure the voltage drop on the contact resistance.  The red and black alligator clips are coming from the generator, the probe is going to channel 1 of the oscilloscope.  There is another cable not shown in the picture, cable going from the generator straight to the oscilloscope for synchronization.





The voltage drop on the banana plug is in the mV range, and the signal is very noisy.  This is the signal without averaging and synchronizing:





Same signal synchronized:





And finally, the same signal locked and averaged for 1024 traces.  Notice how all the noise has gone, and the oscilloscope can measure the Vpp without any problems:



All the noise has vanished because by synchronous averaging, the signal to noise ratio improves by \$\sqrt{N}\$ times, where \$N\$ is the number of averaged traces (here 1024).

In case you wonder what was the contact resistance for those bananas, not very good, in the ballpark of 25m\$\Omega\$:

[jonpaul]

Scope averaging is NOT same as lock-in amp, which uses a PLL.

Suggest to study ensemble averaging definition and lock in amp app notes eg from Stanford Research Labs.

Finally the binding post R tests are not meaningful unless you first clean off all corrosion.

A 4 terminal DC or 1 kHz bridge can easily measure to resolution 1 mOhm.

Jon

[RoGeorge]

Scope averaging is NOT same as lock-in amp, which uses a PLL.

Suggest to study ensemble averaging definition and lock in amp app notes eg from Stanford Research Labs.

Finally the binding post R tests are not meaningful unless you first clean off all corrosion.

A 4 terminal DC or 1 kHz bridge can easily measure to resolution 1 mOhm.

Jon

The role of the PLL here is played by the triggering circuit of the oscilloscope.

I'm aware about the classic implementations, and have been warned before about the synchronous averaging as not being the same as a lock-in amplifier, but I am still convinced they are.  Either way, by analog multiplication and PLL, by polarity switching, by DSP, or by a trace averaging oscilloscope, the basic principles to me remains the same:
- synchronous averaging is preserving the parameters of the measured signal
- noise averaging tends to zero with time
therefore I will say they are equivalent.

They are not 100% the same, I agree with that.  For example a lock-in amplifier is averaging all the consecutive alternances of a signal, while the oscilloscope might skip some of them between triggerings.  Still, the end results remains the same, because the noise is always random and the signal of interest is constant, so it doesn't matter if we skip forward.

Also the functionality remains the same, we can still use this to recover a signals from noise, or as a very narrow band pass filter (comb filter to be more precise), same as with a classic lock-in amplifier.

The advantage when using this oscilloscope technique is we can also see the waveform (which a classic lock-in amplifier doesn't show), and we can use any shape of signals, not only sinusoidal ones.

I could name it "RoGeorge averager" , the amazing lock-in amplifier that shows the waveform, too!

But that would be even more offending, I guess, and most probably I'm not the only one (neither the first) using an oscilloscope this way.  And then, will need to re-explain to everybody when it is advantageous to use it.  By keeping the lock-in amplifier name, one knows in a glimpse in which situations this can be used.


Indeed, there are many ways and many instruments that can measure contact resistance.  This was just an example to show how incredibly well this technique performs in practice, with real signals and real noise, not just in theory.

[2N3055]

You are not synchronously band pass filtering but synchronously  low pass filtering. Low frequencies will skew your averaged signal.

DSP equivalent of lock in would be to use FFT or Goertzel algorithm to band pass filter with very narrow band and then use amplitude of that peak for measurements... And create software PLL equivalent that will lock input frequency the one measured..

[jonpaul]

100% agree  with 2N3055,

the Lock In amp synthesizes a super high Q BP filter so the locking signal (int or ext) is the ONLY signal at the output.

Q 10K...1M are possible.

The ensemble averager is NOT synchronous and the trigger is NOT a lock in but for convienience in viewing a periodic signal.

Suggest to check app nots/texts/articles on Lock In Amps vs Ensemble averaging.

Jon

[nfmax]

You are not synchronously band pass filtering but synchronously  low pass filtering.

It is actually multiple bandpass filtering: the passbands are at the trigger frequency and its harmonics (up to the bandwidth limit of the oscilloscope). The width of each passband is set by the time record length. There is also a passband, of half this width, at DC. This may give problems in the presence of drift, but using an AC excitation as RoGeorge does, and AC coupling the input to the oscilloscope, avoids them.

It's an old book, but see T. H. Wilmshurst, Signal recovery from noise in electronic instrumentation. Bristol ; Boston: A. Hilger, 1985. ISBN 0-85274-783-7. Based on the lecture course he first gave to us unwashed students a few years previously!

[2N3055]

You are not synchronously band pass filtering but synchronously  low pass filtering.

It is actually multiple bandpass filtering: the passbands are at the trigger frequency and its harmonics (up to the bandwidth limit of the oscilloscope). The width of each passband is set by the time record length. There is also a passband, of half this width, at DC. This may give problems in the presence of drift, but using an AC excitation as RoGeorge does, and AC coupling the input to the oscilloscope, avoids them.

It's an old book, but see T. H. Wilmshurst, Signal recovery from noise in electronic instrumentation. Bristol ; Boston: A. Hilger, 1985. ISBN 0-85274-783-7. Based on the lecture course he first gave to us unwashed students a few years previously!

Thank you for very nice comment. You actually explained what I had in mind (English is not my native language).

I was referring to DC drift, and very low frequency components. You are correct that AC coupling will help with this. But still, with all that, it is not gonna come close to Q factor of Lock-in amp. And it will be better at some frequencies etc etc..

It will still be very useful and will help in many occasions to help seeing signal. That is not questionable.

Fun fact is that a DSP code could be made that uses scope capture to mimic lock-in amp behaviour.

Thanks for the book reference.. I will try to take a look.

Regards,

Siniša

[David Hess]

There are some significant differences:

1. A lock-in-amplifier integrates its input over time.  The DSO samples its input synchronously with the trigger.

2. Integration by the lock-in-amplifier causes harmonics to cancel out while sampling synchronously with the trigger by the DSO results in detecting harmonics just as well as the fundamental frequency.

I do not often use a lock-in-amplifier, except in the form of synchronous detection in circuits, but triggering an oscilloscope and using averaging to remove noise is a regular extersize.

[nfmax]

To make the oscilloscope as much like a lock-in amplifier as possible, ensure the excitation waveform fits an exact integer number of times into the time record, and use the scope's FFT function to measure the amplitude of the fundamental frequency. If available, use the flat-top window, to avoid amplitude errors from the windowing, though these should be minimal if the fit is exact.

Some lock-in amplifiers - even analogue ones - could operate as matched filters, correlating using a reference signal having multiple harmonics, for the last n'th of SNR improvement.

I forgot to mention the book Lock-in amplifiers: principles and applications now available online at https://www.sites.google.com/site/lockinamplifiers/home

[SilverSolder]

As long as the excitation signal is a clean sine wave and the DUT doesn't distort it unduly, it seems to me that scope averaging comes pretty close to a lock-in amplifier except that it isn't as sensitive.

I have used a 40dB amplifier in front of the scope to boost sensitivity when using the scope as a pseudo lock-in amplifier in this way.


Another cool thing you can do is display two channels on the scope,  one being the original excitation wave and the other being the measured signal.  This way, you can see the phase shift between the two, so you can be sure that you are measuring pure resistance (as opposed to capacitive (or inductive) reactance).

This setup works great as a detector in a bridge measurement too, with the two-signal phase display trick.  Here, you can use a variable capacitor to balance out the stray capacitance and get the phase spot on for ultra accurate measurements.

Who knew DSOs were so much fun! 

[arivel]

Hi everyone . I read this article but I'm not sure I understood everything.
To avoid causing damage, before proceeding with the measurement with the method described, I thought I would attach a diagram of my circuit so you can tell me if it is correct.
the coil you see actually functions as a current sensor.
The photograph is attached. the toroidal supports are made of plastic material.

[Sensorcat]

Interesting examples of modern digital lock-in amplifiers based on ADC and FFT:

https://www.zhinst.com/europe/en/instruments/product-finder/type/lock_in_amplifiers

Can be used as scopes, too.

[arivel]

Can't you give me an opinion on the correctness of the circuit connections?

[RoGeorge]

I didn't understand what you are trying to measure.  It depends on the amplifier if that is safe or not.  Some amplifiers are connected in a bridge, and in that case it might not be safe to connect the oscilloscope as in your diagram.  There are other things unclear, and that would be unrelated with the topic here.

My advice for you would be to open a new topic, and tell there what your goal is about the measurement.  Attach the pictures, but also tell what you want to achieve, what's the plan with it, what do you want to find out about the amplifier under test.

Depending on all those details, there might be other better ways to measure.

[arivel]

I wrote here because logic itself suggests it and it seems like the most suitable place.
I'll try to explain in words and then if that's not enough I'll open a new topic as recommended.
I would like to measure what comes out of the current sensor seen in the photograph.
it is a Rogowski coil variant. in my case there are many toroids of plastic material, each of them is wound by a coil of enamelled wire, all the coils are connected in series to each other. all the toroids are crossed internally by the conductor which transposes the electric current. Even if it cannot be seen from the photograph, the conductor is electrically insulated with respect to the coils.
the conductor is connected in series to an 8 ohm rheostat and the current is run from an old kenwood k50 audio amplifier
https://www.hifiengine.com/manual_library/kenwood/ka-50.shtml
I don't have the circuit diagram but looking at them they seem to me to have outputs with a ground reference, not a bridge.
the signal frequency is 50 Hz and is the same as the 220 volt power supply of the system distributed in the room. as you can understand, when I pass current, I get a very small and very noisy signal at the coil outputs.
This is what I need the method described here for, I want to see a clean signal on the oscilloscope.
I think everything is quite clear now.

[RoGeorge]

I don't know that amplifier, but if you think it's OK to connect the ground probe of the oscilloscope to the ground output wire of the amplifier, then follow the next steps.

1. Synchronize your oscilloscope from the probe on the left side of your drawing.  That probe will be the reference signal (it should have a strong and clean signal), and it should appear clean on the oscilloscope.  Now connect the probe on the right, and that should show a small and noisy signal.

2. All you have to do now is to put the oscilloscope acquisition in the "Averaging" mode.  The "average" menu depends on the oscilloscope model, so in case you don't know where that is, you'll have to look in the user manual for your oscilloscope.  For my oscilloscope, a Rigol DS1054Z, for the averaging mode I need to press the "Acquire" button, then from the first grey button on the right hand side of the oscilloscope display, select Mode to "Average".

3. Once the Acquire Mode is set to Average, the noisy signal from the coil should become clean.