MSP430 and ADC

[Jon86]

Alright so I've spent a bit of time on this, and I've finally got some pretty simple code going that's doing exactly what I want it to do
I know this probably isn't that orthodox, I don't know, I think Dave may have done it with his DAC program, but I'm clocking the SPI bus bit by bit in a for loop, and putting each bit into the variable. I'm just going to send the raw code to the software, along with the sign and extended range bit, and do all the calculations afterwards.

I'm actually quite surprised how easy it is to do without any library, it worked first time and now I can super easily change how many bits I have, and which of the signal bits I'm using. I guess now I've done it once I can do it with any ADC Thanks for the help guys.

[dannyf]

I guess now I've done it once I can do it with any ADC

Basically. The experience was painful and at time you might be tempted to give up. But in the end, you learned to read the datasheet and program the chip to the datasheet, which is a skill that will keep giving for the rest of your life.

You get a lot more out of this than if someone had given you the answer.

[Jon86]

I guess now I've done it once I can do it with any ADC

Basically. The experience was painful and at time you might be tempted to give up. But in the end, you learned to read the datasheet and program the chip to the datasheet, which is a skill that will keep giving for the rest of your life.

You get a lot more out of this than if someone had given you the answer.

Yeah I really understand what I'm doing now. To be honest I've found it infinitely easier to read each byte individually and toggle the clock pin and so on, rather than just using a library. Also means I can read any bit that I want and do separate operations with it.

[tszaboo]

the correct term is bit-banging. I really hope at some point we will use the hardware exclusivly this way ,with multiple high speed cores (200mhz). Kinda like xmos already does.

[dannyf]

rather than just using a library.

Your bit-banging routines can be made into a library as well. It helps with code clarity, readability and reliability.

[Jon86]

So you're saying that the way I've done it isn't impractical and sluggish?

[dannyf]

I didn't see how you did it so it would be with basis for me to say if it is sluggish / fast or impractical / practical.

I was simply commenting on the fact that you can write your own library to help improve various aspects of your code.

[Jon86]

I didn't see how you did it so it would be with basis for me to say if it is sluggish / fast or impractical / practical.

I was simply commenting on the fact that you can write your own library to help improve various aspects of your code.

Ah fair enough, well here's my code if you wanted to have a look, it'd be interesting to see what you think.
Obviously this is the first time I've ever done anything like this, so sorry if the code is a bit messy.

Code: [Select]

//Set up communication pins
int CS = 7;
int MasterIn = 6;
int SCLK = 5;
int EXR = 0;
int sign = 1;

//Set up variables
int i;
int shift;
long buffer;
long result = 0;

void ClockToggle()
{
  //Set clock high, pause and low again
  digitalWrite(SCLK, HIGH);
  delayMicroseconds(10);
  digitalWrite(SCLK, LOW);
  delayMicroseconds(10);
}

void setup()
{
  Serial.begin(9600);
 
  //Set up IO
  pinMode(CS, OUTPUT);
  digitalWrite(CS, HIGH);
  pinMode(MasterIn, INPUT);
  pinMode(SCLK, OUTPUT);
  delay(500);
}

void loop()
{
    digitalWrite(CS, LOW);
    result = 0;
    delayMicroseconds(2);
    //Clock through bit 31 and 30
    ClockToggle();
    ClockToggle();
    //Read sign bit
    sign = digitalRead(MasterIn);
    ClockToggle();
    //Read extended range bit
    EXR = digitalRead(MasterIn);
   
    for(i=1; i<24; i++)
    {
      ClockToggle();
      buffer = digitalRead(MasterIn);
      shift = 24-i;
      result |= buffer<<shift;
    } 
    Serial.print(sign);
    Serial.print(",");
    Serial.print(EXR);
    Serial.print(",");
    Serial.println(result);
    //Deselect Chip
    digitalWrite(CS, HIGH);
    delay(160);
}


[dannyf]

This is not very efficient:

1) you don't need 10us delay -> the datasheet should have specifications for minimum pulse width and it is unlikely us or more.
2) I would write a routine that read them a byte at a time, using the shiftIn() (?) library or roll your own.

It would look something like this:

Code: [Select]


unsigned long ltc2400_read(void) {
  unsigned long tmp=0;
 
  digitalWrite(LTC2400_CS, LOW); //pull cs low - idles high
  tmp = shiftIn(...); //read the msb (bit31..24)
  tmp = shiftIn(...) | (tmp << 8);  //read the 2nd byte (bit 23..16)
  tmp = shiftIn(...) | (tmp << 8);  //read the 3rd byte (bit 15..8)
  tmp = shiftIn(...) | (tmp << 8);  //read the last byte (bit 7..0)
  digitalWrite(LTC2400_CS, HIGH); //pull cs high -> start next round of adc
  return tmp; //read tmp
}

...
  //read ltc2400
  do {unsigned long tmp = ltc2400_read();} while (tmp & LTC2400_EOC); //read ltc2400 - wait for the conversion to end
  sig = tmp & LTC2400_SIG; //retain the signage
  exr = tmp & LTC2400_EXR; //retain the signage
  signed long ltc2400_adc=tmp & (0x0ffffffful); //strig adc of the signs
  if ((~sig) & exr) ltc2400_adc=-ltc2400_adc; //input is negative - sub-digits retained in ltc2400_adc

The resulting number is a signed long and retains all the digits from the adc + sign.

[dannyf]

After that piece of code is debugged, you can then move it to .h/.c files for use in future projects, knowing that it is fully debugged.

[miguelvp]

You can even go crazy and turn the value directly into a double.
So I'm going to flex my programming muscles and sorry if I loose you, but hopefully you and others can get something from this quite long reply.

Disclaimer, I'm a noob at electronics but not at coding, but I might make a mistake since I'm not even going to compile this to see if it does what I think it does.

So lets start by declaring some not too obvious C structures (they also work for C++).

Code: [Select]

//
// Create a double, little-endian sample. i.e. Intel (NOT Motorola that would be big endian.)
//

// Define a single bit to fit on an unsigned 64 bit long.
typedef unsigned long bit:1;

// Define a structure used to access bits individually from 0 to 63.
// not really needed but added for completeness.
typedef struct {
   bit bits[64];
} b_section;

//
// Define a structure that splits a double in sections so we can construct them from the different parts that form them.
//
// Double Precision Float notes, taken from IEEE 754 i.e. wikipedia
//
// If exponent is 0x000 is signed zero if mantissa is 0 (-0)
// If exponent is 0x000 then is a subnormal if mantissa is not 0.
// If exponent is 0x7ff then is infinite if mantissa is 0
// If exponent is 0x7ff then is a NaN (Not a Number, ie. 0 divided by 0) if mantissa is not 0.
//
// Exponent is 1023 biased (0x3ff).
// Value if exponent is > 0x000 and <0x7ff, then mantissa has a [1.] implied
// -1*(sign)*2^(exponent-1023)*[1.]mantissa
// This is what we want for values equal or greater than 1.0 (denoting Vref+1LSB or higher)
//
// Value on sub normals (if Exponent is 0 and mantissa is different than 0)
// -1*(sign)*2^(1-1023)*[0.]mantissa
// This is what we want for the range less than 1.0 and into the negative.
//
// Example values from wikipedia:
// 0000 0000 0000 0000 = 0
// 8000 0000 0000 0000 = -0
// 7ff0 0000 0000 0000 = positive infinite
// fff0 0000 0000 0000 = negative infinite
//

// Little endian so less significant bits go first.
typedef struct {
unsigned long mantissa:52;
unsigned long exponent:11;
unsigned long sign:1;
} d_section;

typedef union {
double    val;
b_section b_val; // b_ for bit value
d_section s_val; // s_ for sections value
} convert_to_double;

Note that a union allows you to see a memory location in different ways. So if you wanted to access bit 0 of a convert_to_double value you can access it by value.b_val.bits[0], or access bit 63 with value.b_val.bits[63]

Now that we have all those structures and the converting union defined, you read your full 28 bit value (including the sub less significant bit (subLSB) 4 bit value data) as well as the sign and the extra range. First declare your result value of type convert_to_double and also declare the extended range variable for later use.

Code: [Select]

   convert_to_double result;
   int extendedRange;

Then, going to your old code (you can adjust this to your newer code if you want) read the whole 32 bits of data, but now we need the space and the default int (32 bits usually) is signed, so we need to go for a long and better make it unsigned. Even if the top two bits are 0 and it shouldn't flip the sign but just in case.

Code: [Select]

   unsigned long in = SpiRead(); // input must be an unsigned long make sure SpiRead returns an unsigned long as well.

Now you can assign the sign signal to the result (0 for positive in the double, 1 for negative in the double).
Lets assign the extended range as well (1 for True, or 0 for False for later use).

BTW this code:

register = (condition_to_evaluate)? value_if_true : value_if_false;

is the same as:

if(condition_to_evaluate)
   register = value_if_true;
else
   register = value_if_false;

Note, don't use the construct with macro definitions, because it usually yields to bad behavior, but on normal constructs it should be just fine.

Code: [Select]

   result.s_val.sign = (in&0x20000000ul)?0:1; // bit 29 is 1 when positive, undetermined right at 0V and 0 when bellow 0V
   extendedRange = (in&0x10000000ul)?1:0; // bit 28 is 1 if outside 0-Vref, 0 if within range.

If we want Vref to represent the value 0.99999999999(9) (within range where under parenthesis means periodic) and 1.0000(0) to represent Vref+1LSB (outside of the range) then we need to use the mantissa as a sub normal. (meaning that we have to force the exponent to be 0. We know this is true if the sign is positive (result.s_val.sign == 0) and if we are not on the extended range.

Code: [Select]

   // Subnormal between 0 to 0.9999 [.0] implied before mantissa will take the value 0, otherwise 1023 to imply [1.] before mantissa
   result.s_val.exp = ((result.s_val.sign == 0)&&(extendedRange == 0))? 0 : 0x3ff;

Note i'm using the logical and (&&) the bitwise and (&) will work too but makes it look strange, I could make it shorter and faster but then it would be bit harder to read.

For example:

Code: [Select]

  result.s_val.exp = (result.s_val.sign|extendedRange)? 0x3ff : 0;
That would read if sign or extended range then exponent is biased by 1023 otherwise use subnormal.
And that is fine and faster to compute, so use it instead if you want.

Edit maniac added:
Let's make it a bit faster but more obscure coding.

Code: [Select]

  result.s_val.exp = (result.s_val.sign|extendedRange)*0x3ff;

Almost there, we just need to put the mantissa in place.
So we have 28 bits (including the extra 4 subLSB bits) and the mantissa can hold 52.
So we need to shift to the left by the difference in precision, in our case is 52-28 so it's 24 left.

Edit: noticed I forgot to mask off the higher 4 control bits so I fixed it

Code: [Select]

   // Adjust reading into the mantissa.
   result.s_val.mantissa = (in&0xffffffful)<<24;

Now if you don't want the low 4 bits, you still shift by 24 but you mask the 4 bits first.

Code: [Select]

   // Adjust reading into mantissa discarding low sub LSB 4 bits.
   result.s_val.mantissa = (in&0xffffff0ul)<<24;

A note for shifting: Since you are on base 2 (binary) if you shift right you divide by powers of 2, if you shift left you multiply by powers of 2. Most people think about the truncation side of shifting but shifting makes fast dividers/multipliers (as long as it's a power of 2 you want to multiply or divide by).

Edit(nth) yet another edit to clarify one thing. So if you were doing this in assembly instead of C you will have the choice to rotate left with carry and other shift assembler instructions. it wont matter much other than the less significant bit will either stick while shifting or become 0, think about it as a math floor function or a ceil (ceiling) function. But in this context it wouldn't make a difference.

So what do you get after all this?

Well, you can access the double directly, say you want to return the value read, then you will return the following double (your function will have to be declared to return a double value as well).

Code: [Select]

   // Return read value. Range will be from -0.125 up to 1.125.
   // [-0.125 to 0.0) for extended negative range.
   // [0.0 to 1.0) for within range
   // [1.0 to 1.125] for extended positive range.
   // multiply the value by Vref to obtain the actual voltage.
   return result.val;

And there you have it, sorry for the length and detail of this, I hope it helps not just you and I also hope I didn't make any horrendous coding mistake, but like I said, I didn't test this or tried to compile it.

Edit: on the last code (the return value) in the comments about the range, the square bracket "[" means included, the parenthesis "(" means excluded.


One more Edit:
If you want to print the double you can do so with

  printf("Input as in percent of Vref = %lf\n",result.val);

Yet one more edit:
This code assumes 1 byte data alignment, some programs change that and that can mess up the structure and the union.

Yet one more edit edit:
To help with the visualization here is an image that shows the double:


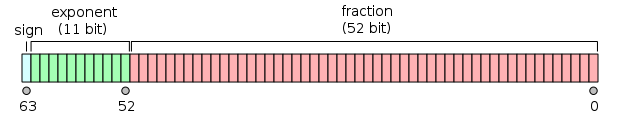
You can modify this to use floats instead but more constrained.
32 bits total.
8 bits exponent bias is 127 from the value depicted on the field
23 bits mantissa so you will have to stick to the 24bits and truncate one of those as well.


Apologize for the many edits, just correcting erratas as any good engineer (even if it's software) should do!
Also just noticed that this will allow for positive and negative 0 I think, so when the datasheet mentions the sign is undetermined at 0, this will gracefully handle it. (Not!, read bellow)

You can also define new structures to add into the union, like the full 64 bits divided by nibbles (half a byte or 4 bits), bytes, words and double words. then you can use those to help you read the data in more directly, reducing time.

Ok, last edit I swear, but I'm really not sure on the undetermined sign bit flip at 0 volts and had plenty of wine so I don't want to think about it. but if sign is is 1 (positive or 0 in the on the double bit field) and and the extended range is 0 then the exponent is the subnormal, meaning implied [0.]mantissa or 0, but if the sign flips to 0 (negative or 1 on the sign bit field in the double) and the extended range is 0, then the exponent will be the normal exponent implying [1.] so figure out how to solve that edge case, because it will spike to -1*Vref when it's really 0. You can add the mantissa being 0 to determine using the subnormal exponent or not. (expensive at 52 bits compare to 0, well not really if the compiler does the right thing and can use the z flag after some operation with the mantissa holding register to determine if it's 0 or not).

Anyways, that will fix it but don't use it as illustrated above because the bug (-1Vref spike) will be hard to find.

[Jon86]

Awesome, thanks for the help
There's a lot to understand there, but I think I got a good majority of it

[BravoV]

miguelvp, much appreciated, great post you've done there , especially for coding noob "AND" electronics noob like me.   

Your post there is now bookmarked.

[miguelvp]

Thanks guys, I guess I went a bit overboard but hopefully when I need help on electronics I don't get the RTFM treatment I always read them!

BravoV, if you bookmarked it, please note that the comments of the readings apply to the datasheet of the LTC2400 24-Bit ADC chip.

Other ADCs will change parameters.

Also if going to float (loosing just one bit precision) all the sample has to be adjusted including the structures and the union.

Edit: yes i'm an edit fiend! No disrespect on the RTFM or the you should learn the hard way guys, but I don't expect someone to catch up with me after 30 years of programming, I rather teach than enforce!

like my son says.... peace out (hopping no flame war i think, but speaking my mind never the less)

[BravoV]

BravoV, if you bookmarked it, please note that the comments of the readings apply to the datasheet of the LTC2400 24-Bit ADC chip.

I'm pretty confident majority of the electronics tinkerers that are interested with precision ADC, must at least read LTC 2400 datasheet once in their life. 

Yes, I'm very familiar with LTC 2400 datasheet.

Edit: yes i'm an edit fiend! No disrespect on the RTFM or the you should learn the hard way guys, but I don't expect someone to catch up with me after 30 years of programming, I rather teach than enforce!

Hence, thats why I bookmarked it instead of saving it off-line. 

Reading your posts there, I had a feeling you're the type who loves to mentor noobs, which is quite rare these days.    (mentoring != spoon feeding)

[miguelvp]

Edit: yes i'm an edit fiend! No disrespect on the RTFM or the you should learn the hard way guys, but I don't expect someone to catch up with me after 30 years of programming, I rather teach than enforce!

Hence, thats why I bookmarked it instead of saving it off-line. 

Reading your posts there, I had a feeling you're the type who loves to mentor noobs, which is quite rare these days.    (mentoring != spoon feeding)

Don't get me wrong I can tell between noobs and I won't put the effin effort to learn this crap. But yeah, even if the young people where I work at think they can do better than me, they really don't know what I'm capable off, it's beyond their realm.

So why will I want to get someone to learn the hard way (i.e. before the internet) when now re-enforcing and spreading the knowledge is (or should be) the norm!.

Granted, we used to push pixels at 300 baud, not they get pushed faster but.... when we couldn't push them faster we figured ways to optimize them, so z80 3.25 MHz (zx81 my first owned computer) to say 3 GHz now with 8 cores and hyperthreading so virtually 16 core pipes and GPU multi processing?... it doesn't matter!!!! same principles back then apply now, meaning. I don't have to push pixels as efficiently as I did before, but. If I do? then.. i'm pushing pixels faster than the competition.

So I'm a bit over half a century old, so what, I forgot more things than kids learn now. And by forgot I mean, I learned them so if I have to be exposed to it again I'll pick it up way faster than anyone.

Go guess one thing... nah I'll tell you, English is my 4th human language, but Basic as my 1st computer one then C, C++ etc... The first game I made required (I think) a 56K modem to race motorcycles online for 30 people playing at the same time and with roger wilko (voice protocol) at the same time and this is 14 years ago, now they can't do that with who knows how many Megabits per second from you home.

My point again is teach, specially the old ways. Spartan or the KISS framework (keep It Simple Stupid) like Lotus did (yes I'm lucky enough to have such a fine spartan nonsense vehicle that can do 0-60mph in 4.7 seconds with just a 190 horsepower engine.

My point (again) is that throwing cycles doesn't matter if you waste most of them. Then again I live in Chicago so my car has been in the garage for over a year and I might sell it because I don't want to put it through this town's nightmares.

Don't get me wrong, love Chi-Town (or Chi-beria) like they've been calling it this last months. But I don't really need to drive anymore and I rather pay for the garage than to drive my car. Would be like measuring an e-bay power supply with a 66 GHz oscilloscope like the signal tap guy did ended up watching netflix (futurama I think) on the half a million dollar scope.

Ok so I'm way rambling toughts, don't care really. my point is this. Keep teaching and passing on information. For my Country, keep those high level University students here, they are taking our knowledge away (I mean seriously that should be NSA's most important thing ever!)

Now we are teaching them (yes I still believe we have the best Universities our there!) but now instead of staying here they are going back home?? that's is just messed up!

Not because they want to go back, just because at their age, I rather stay here since the mindset was beyond anywhere in the planet.

Ok. Not turning into politics so I'm done. Yeah wine is not helping the cause but at least you are getting my raw thoughts, as it should be.

[dannyf]

You can even go crazy and turn the value directly into a double.

Why do you want to do that?

[miguelvp]

You can even go crazy and turn the value directly into a double.

Why do you want to do that?

Because you can do more with a normalized real number (0 to 1) than an integer?

Specially when you are keeping all the precision of your input signal and have more room to spare without loosing the signal integrity?

Also you could do some fancy DSP functions on the resulting value, I don't know what he is trying to measure, but converting it to a normalized value that multiplied by Vref gives you the actual voltage.

And if you read the full post, you'll realize that it will use the extended range of the chip including the 12.5% under 0V and over Vref...

Code: [Select]

  // Return read value. Range will be from -0.125 up to 1.125.
   // [-0.125 to 0.0) for extended negative range.
   // [0.0 to 1.0) for within range
   // [1.0 to 1.125] for extended positive range.
   // multiply the value by Vref to obtain the actual voltage.
   return result.val;


[dannyf]

Because you can do more with a normalized real number (0 to 1) than an integer?

For that, you are willing to incorporate 64-bit floating point math on a 8/16bit machine with often limited ram?

I can do all of that in 32-bit integer math. No, thanks.

[tszaboo]

You can even go crazy and turn the value directly into a double.

Why do you want to do that?

Not to mention you need extra good reference, precision components, layout and everything to get more than 16 noise free bits. You might need float for calculations, but even that is enough for a 8.5 digit multimeter grade measurements.

[paf]

You can even go crazy and turn the value directly into a double.
So I'm going to flex my programming muscles and sorry if I loose you, but hopefully you and others can get something from this quite long reply.

Disclaimer, I'm a noob at electronics but not at coding, but I might make a mistake since I'm not even going to compile this to see if it does what I think it does.
.......

Sorry, but could you please not write this kind of stuff?

When you have a 16 bit processor using floats is a BIG performance mistake.  Also it is very easy to understand integer arithmetic, but doing your own floating point operations in a correct way is very hard  (and slow) in a 16 bit processor.

Just because you can do floats does not mean that you should do it.

Caveat:
      In a 32 bit processor in C, converting from an int to a float, you may loose precision.


 

[suicidaleggroll]

When you have a 16 bit processor using floats is a BIG performance mistake.

Especially when there is no math/floating point co-processor.  Not only does it slow things WAY down, it also bloats your code by about a half a kB when it has to bring in all of those floating point libraries.  Considering many msp430 models only have single digit kBs of flash to begin with, that's a big impact.

[vvanders]

Caveat:
      In a 32 bit processor in C, converting from an int to a float, you may loose precision.

Not to pile on the bandwagon(because I appreciate that the op took the time to explain things) but a float -> int conversion will also stall on many architecture that do have a dedicated FPU. It's best to keep things on one domain or the other.

[miguelvp]

Apologies to all,

I was focusing more on the actual LTC2400 chip than the processor he was using so I got carried away when I noticed the mapping from the input of the chip just is so easy to convert to a double (or a float).

I should have read the MSP430 datasheet, and somewhat thought it was an ARM based microcontroller, but I guess it is not. (I'm a noob at electronics after all)



But it will still be useful for others that have processors with DSP and floating point capabilities, or at least to understand some things.

Btw, floats and doubles are easy and fast to operate with regular processors as well specially if they are denormals (with out the assumed [1.] before the mantissa.) or at the range that we are talking about in here.

You are really just operating them the same as you will any integer, and you can use the carry bit to extend it to multi byte operations.

Multiplications are just shifts and adds when the bit is 1 or  go to the next when is 0. Also there are fast ways to do adds and multiplies in subsections if you have integer multiplication and division built in.

Divisions are just multiplications with inverse, but I guess using vanilla libraries suck oh well, lesson learned.

Back to my FPGA I guess, were I could do these operations with no problems at all at the cost of power of course!

Again sorry for misleading the OP but I did see some floating point being use on his code and the mention of double precision by others. Next time I'll keep it to myself.

[BravoV]

But it will still be useful for others that have processors with DSP and floating point capabilities, or at least to understand some things.

Well, at least for me, your long post there actually quite useful since I use ARM M4F 80 Mhz core (still learning though  ) which has a dedicated FPU and with all the whole shebang for hardware based floating point operations in it.