how to properly generate ideal sine test sample?

[radiolistener]

Basically I need a test vector with ideal sine wave, it should be 14 bit integer format and consists of 16 samples (a single sine period with maximum amplitude). I'm expecting symmetric AES17 sample representation which means that the max negative value is not used (for symmetry) and mean value should be 0.

Previously I was used test vector provided by another people, I don't know how it was generated, but it seems that this vector provides better sine performance than I can generate. Here it is:

Code: [Select]

0
3134
5792
7567
8191
7567
5792
3134
0
-3134
-5792
-7567
-8191
-7567
-5792
-3134

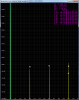
And it's spectrum:


Now I'm trying to generate the same sine with code in the following way:

Code: [Select]

var bits = 14;
var halfRange = Math.Pow(2, bits-1);
for (var i = 0; i < 16; i++)
{
    double sine = Math.Sin(2 * Math.PI * i / 16);
    sample[i] = round( sine * (halfRange - 1D) );
}

sine * (halfRange - 1D) result:

Code: [Select]

0.0
3134.5599945024505
5791.91164469901
7567.49725079995
8191.0
7567.49725079995
5791.911644699011
3134.5599945024514
0.0000000000010030750644159092
-3134.5599945024496
-5791.91164469901
-7567.4972507999482
-8191.0
-7567.4972507999491
-5791.911644699012
-3134.5599945024555

and after round I get this:

Code: [Select]

0
3135
5792
7567
8191
7567
5792
3135
0
-3135
-5792
-7567
-8191
-7567
-5792
-3135

And it's spectrum:


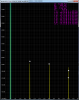
It seems that my sine has a little worse performance, it has -87.91 dB for 3'rd harmonic, while first sine has -95.83 dB for 3'rd harmonic.

Both test vectors almost the same, the only difference is 3135 instead of 3134. But I have no idea how to obtain 3134 value, because 3134.5599945 should be rounded to 3135. And if I replace round with floor (cut-off fraction part), I will get incorrect value for the third value, because 5791.91 will be rounded to 5791, but it should be 5792...

So there are two questions:
1) Is the first sine really has better performance? (maybe my spectrum calculation is just not so accurate)
2) How to calculate it with proper rounding?

[asmi]

1. There is no such thing as "the ideal sine wave". It's a purely mathematical construct.
2. 14 bits gives a resolution of 1/(2^14) = 6.103515625 * 10^-5, which gives an error of 20 * log (6.103515625 * 10^-5) ~ -84.3 dB. So unless I screwed up the math somewhere (again ), you can't really get anything much better than that with this format.

[SiliconWizard]

Indeed.
The fact you seem to be getting "better performance" with actual rounding errors (if I get what you said correctly) is marginal. It's probably the result of an additional rounding error from the spectrum analysis itself that happens to give a more favorable figure.
As asmi said, you can't get better with 14 bits.

[asmi]

As asmi said, you can't get better with 14 bits.

Technically you could've gotten two times better result (about -90.3 dB) if ADC would be able to do a proper rounding (round-to-nearest), but as far as I know all of them round down, which is why the max error is 1 LSD, not 0.5 LSD which would be the case for round-to-nearest rounding. But in any case ~-90.3 dB seems to be the absolute best case possible, so not sure how he got better numbers.

[radiolistener]

1. There is no such thing as "the ideal sine wave". It's a purely mathematical construct.

I understand discrete signal dynamic range limit and quantization noise. But the goal is not to bypass this limitation. The goal is to get sine with minimum possible distortion for specific resolution.

2. 14 bits gives a resolution of 1/(2^14) = 6.103515625 * 10^-5, which gives an error of 20 * log (6.103515625 * 10^-5) ~ -84.3 dB. So unless I screwed up the math somewhere (again ), you can't really get anything much better than that with this format.

Dynamic range 6.02*14 = 84.28 dB represents dynamic range of worst case for any possible signal. It is limited due to quantization noise at -84.28 dB level. But I'm talking about specific sine, which performance depends on error between aperture and actual sine points, so its actual performance will depends on a bit resolution and relation between sine frequency and sample rate.

I need a discrete sine wave which best fits with continuous sine for selected bit resolution. The criterion here is a minimum possible harmonics/distortion level after waveform reconstruction from discrete to continuous representation.

But in any case ~-90.3 dB seems to be the absolute best case possible, so not sure how he got better numbers.

Reconstructed wave dynamic range exceeds theoretical -84 dB noise floor because errors (due to misalignment between discrete points and aperture) is not maximum possible for selected combination of sine parameters, bit resolution and sample rate.

For example 14-bit 96 kS/s DC signal (constant sample value) has zero noise, so it has infinite dynamic range which is much better than mentioned 84.28 dB for 14 bit.  But you cannot get the same result for any kind of signal. While 84 dB limitation means guarantee that 14 bit resolution can represent at least 84 dB dynamic range signal in worst case for any signal. That limitation is for worst case. As mentioned, for DC signal it will be infinite.

[hamster_nz]

Would you mind looking at this set of values?

Code: [Select]

0  3134  5791  7566  8190  7566  5791  3134  0  -3134  -5791  -7566  -8190  -7566  -5791  -3134

If they are better than the original I'll share the code that found them...

[macboy]

Try scaling very slightly up or down (fraction of one full scale bit). You can find a point where it will round as you want.
Even better, add noise (yes, add) to achieve dithering which can dramatically reduce distortion, at the expense of random noise. If you need substantially less than 0.5 FS bandwidth, then push (shape) the noise up to high frequencies and filter it out.  This is how you can reproduce a -105 dB tone from a CD with theoretically only 96 dB of dynamic range.

[OM222O]

An easy implementation in python is (you can use an online python interpreter):

Code: [Select]

import numpy as np
idx = np.arange(16) # Number of samples per period
sf = idx.max() / (2*np.pi) # scaling factor for the period
arr = idx/sf # create a new array that goes from 0 to 2 pi in N steps
arr = np.sin(arr) # calculate the sin value for each point
integer_arr = (arr*(2**13)).astype('int32') # Scale the array by 2^13 (the actual sine values go between -1 and 1, giving you an effective range of 2, so you need to scale by max int/2)
print(integer_arr)
this results in:
[    0  3331  6087  7791  8147  7094  4815  1703 -1703 -4815 -7094 -8147 -7791 -6087 -3331     0]
you can easily change the number of samples , add phase offset or change the scaling factor etc.

Edit: to change the phase offset just add it to line 5, for example you can do arr = np.sin(arr + (np.pi/2)) to add a pi/2 offset and turn this into a cos table

[BrianHG]

this results in:
[    0  3331  6087  7791  8147  7094  4815  1703 -1703 -4815 -7094 -8147 -7791 -6087 -3331     0]
you can easily change the number of samples , add phase offset or change the scaling factor etc.

2 sequential samples with the value 0 in the 16 phase loop?
Wouldn't that generate substantial distortion?

[SiliconWizard]

Yes, it's 16 samples while the period is computed over 15 samples. Looks like a typical off-by-one issue.

[radiolistener]

Would you mind looking at this set of values?

Code: [Select]

0  3134  5791  7566  8190  7566  5791  3134  0  -3134  -5791  -7566  -8190  -7566  -5791  -3134

If they are better than the original I'll share the code that found them...

wow, it has -105.25 dBc for 3'rd harmonic and -100.25 dBc for 5'th harmonic
Almost all harmonics below -100 dBc, except 7'th which is -99.05 dBc...

How to calculate it?

[OM222O]

this results in:
[    0  3331  6087  7791  8147  7094  4815  1703 -1703 -4815 -7094 -8147 -7791 -6087 -3331     0]
you can easily change the number of samples , add phase offset or change the scaling factor etc.

2 sequential samples with the value 0 in the 16 phase loop?
Wouldn't that generate substantial distortion?

Yes, it's 16 samples while the period is computed over 15 samples. Looks like a typical off-by-one issue.

0 and 2 pi are the same point effectively. If this is an issue you can set the array to be of lenght N+1 and ignore the last value

[radiolistener]

this results in:
[    0  3331  6087  7791  8147  7094  4815  1703 -1703 -4815 -7094 -8147 -7791 -6087 -3331     0]
you can easily change the number of samples , add phase offset or change the scaling factor etc.

2 sequential samples with the value 0 in the 16 phase loop?
Wouldn't that generate substantial distortion?

Yes, just -20 dBc for 2'nd harmonic and the carrier is not full scale, just -0.36 dBc:

[hamster_nz]

Would you mind looking at this set of values?

Code: [Select]

0  3134  5791  7566  8190  7566  5791  3134  0  -3134  -5791  -7566  -8190  -7566  -5791  -3134

If they are better than the original I'll share the code that found them...

wow, it has -105.25 dBc for 3'rd harmonic and -100.25 dBc for 5'th harmonic
Almost all harmonics below -100 dBc, except 7'th which is -99.05 dBc...

How to calculate it?

Just looked one either side of the original samples, for all samples, and picked which is best:

Code: [Select]

///////////////////////////////////////////
// sine_samples.c : hamster@snap.net.nz
//
// A quick hack to see if I can find better
// sine sample values for an ADC
//
///////////////////////////////////////////
#include <stdio.h>
#include <math.h>

static int data[] = {
   0,  3134,  5792,  7567,  8191,  7567,  5792,  3134,
   0, -3134, -5792, -7567, -8191, -7567, -5792, -3134
};

static double evaluate(int data[]) {
   double tc = 0.0, ts = 0.0, t_err = 0.0;

   // Single bin DFT
   for(int i = 0; i < 16; i++) {
      ts += data[i] * sin(i*M_PI*2.0/16);
      tc += data[i] * cos(i*M_PI*2.0/16);
   }
   ts /= 16/2;
   tc /= 16/2;

   // Remove the fundimental and total up RMS of what is left
   for(int i = 0; i < 16; i++) {
     double e = data[i] - sin(i*M_PI*2.0/16) * ts - cos(i*M_PI*2.0/16) * tc;
     t_err += e*e;
   }
   return t_err;
}

int main(void) {
   double min = 0.0;
   int limit = pow(3,16);
   // to pow(3,16) - to try every combination
   for(int i = 0; i < limit; i++) {
      int d[16];

      // Add either +1,0,-1 to every sample, based on i
      int x = i;
      for(int j = 0; j < 16; j++) {
         switch(x%3) {
            case 1: d[j] = data[j]-1; break;
            case 0: d[j] = data[j];   break;
            case 2: d[j] = data[j]+1; break;
         }
         x /= 3;
      }

      // Range check
      if(d[4] > 8191 || d[12] < -8191)
         continue;

      // See if this is any better or worse
      double this_noise = evaluate(d);
      if(i == 0 || this_noise < min) {
         min = this_noise;
         printf("%12.9f: ", this_noise);
         for(int k = 0; k < 16; k++) {
           printf("%5d ",d[k]);
         }
         printf("\n");
      }
   }

   // Print out the original for comparison
   printf("%12.9f: ", evaluate(data));
   for(int k = 0; k < 16; k++) {
       printf("%5d ",data[k]);
   }
   printf(" << original\n");
   return 0;
}

If I lack the skills to do it properly, I just brute-force it! 

Here's the output:

Code: [Select]

$ ./main
 1.527446318:     0  3134  5792  7567  8191  7567  5792  3134     0 -3134 -5792 -7567 -8191 -7567 -5792 -3134
 1.516362543:     0  3135  5792  7567  8191  7567  5792  3134     0 -3134 -5792 -7567 -8191 -7567 -5792 -3134
 1.255278769:     0  3135  5792  7567  8191  7567  5792  3134     0 -3135 -5792 -7567 -8191 -7567 -5792 -3134
 1.188563146:     0  3135  5792  7568  8191  7567  5792  3134     0 -3135 -5792 -7568 -8191 -7567 -5792 -3134
 1.121847524:     0  3135  5792  7568  8191  7568  5792  3134     0 -3135 -5792 -7568 -8191 -7568 -5792 -3134
 1.110763749:     0  3135  5792  7568  8191  7568  5792  3135     0 -3135 -5792 -7568 -8191 -7568 -5792 -3134
 1.023786799:     1  3135  5792  7567  8191  7567  5791  3134    -1 -3135 -5792 -7567 -8191 -7567 -5791 -3134
 0.957071177:     1  3135  5792  7568  8191  7567  5791  3134    -1 -3135 -5792 -7568 -8191 -7567 -5791 -3134
 0.955140664:     0  3134  5791  7567  8190  7567  5791  3134     0 -3134 -5791 -7567 -8190 -7567 -5791 -3134
 0.920336789:     0  3134  5791  7566  8190  7566  5791  3134     0 -3134 -5791 -7566 -8190 -7567 -5791 -3134
 0.920336789:     0  3134  5791  7566  8190  7566  5791  3134     0 -3134 -5791 -7567 -8190 -7566 -5791 -3134
 0.920336789:     0  3134  5791  7566  8190  7567  5791  3134     0 -3134 -5791 -7566 -8190 -7566 -5791 -3134
 0.920336789:     0  3134  5791  7567  8190  7566  5791  3134     0 -3134 -5791 -7566 -8190 -7566 -5791 -3134
 0.506366571:     0  3134  5791  7566  8190  7566  5791  3134     0 -3134 -5791 -7566 -8190 -7566 -5791 -3134
 1.527446318:     0  3134  5792  7567  8191  7567  5792  3134     0 -3134 -5792 -7567 -8191 -7567 -5792 -3134  << original


[hamster_nz]

This might be a tiny bit better, but has a tiny phase shift:

Code: [Select]

1  3135  5792  7567  8190  7566  5790  3133    -1 -3135 -5792 -7567 -8190 -7566 -5790 -3133


[OM222O]

I'm still not sure what the point of this topic is. There are an infinite number of phase shifts you can try and some may work better than others in specific test cases, but you always have some rounding errors. If you want to minimize quantization error that's pretty easy to do mathematically. If you want to generate a specific frequency and phase shift, that's also pretty easy to do, but like others said, there is no "ideal sine wave". You can re-write the program I gave you in any language and get the same results, but it seems pointless to worry about the harmonics noise as they can be filtered out in any good design. What's the main goal of generating the sine table?

The funny thing is that you don't even need a spectrum analyzer to test this, using any FFT analysis tool (numpy supports this) should give you the same results, so you can just simulate the whole thing and optimize it as much as you want, but again, I can't find a good reason for why you should.

Edit: I used 17 samples and ignoring the last 0, this results in almost exactly the same result as you posted initially:
[    0  3134  5792  7568  8192  7568  5792  3134     0 -3134 -5792 -7568 -8192 -7568 -5792 -3134     0]

[Someone]

Would you mind looking at this set of values?

Code: [Select]

0  3134  5791  7566  8190  7566  5791  3134  0  -3134  -5791  -7566  -8190  -7566  -5791  -3134

If they are better than the original I'll share the code that found them...

wow, it has -105.25 dBc for 3'rd harmonic and -100.25 dBc for 5'th harmonic
Almost all harmonics below -100 dBc, except 7'th which is -99.05 dBc...

How to calculate it?

If you dont mind losing some gain:
[0 3107 5741 7501 8119 7501 5741 3107 0 -3107 -5741 -7501 -8119 -7501 -5741 -3107]

Many ways to skin this cat!

[Someone]

If you want to minimize quantization error that's pretty easy to do mathematically.

Except it isnt! The cost function has many local minima, so there is no easy method.

[hamster_nz]

Edit: I used 17 samples and ignoring the last 0, this results in almost exactly the same result as you posted initially:
[    0  3134  5792  7568  8192  7568  5792  3134     0 -3134 -5792 -7568 -8192 -7568 -5792 -3134     0]

... except 8192 and -8192 is out of range.

If your DAC's reconstruction filter is significantly  filtering the 3rd harmonic of f/16 sine wave it might be a little too aggressive... or you don't care about using the full requency performance of your DAC.

[OM222O]

Edit: I used 17 samples and ignoring the last 0, this results in almost exactly the same result as you posted initially:
[    0  3134  5792  7568  8192  7568  5792  3134     0 -3134 -5792 -7568 -8192 -7568 -5792 -3134     0]

... except 8192 and -8192 is out of range.

If your DAC's reconstruction filter is significantly  filtering the 3rd harmonic of f/16 sine wave it might be a little too aggressive... or you don't care about using the full requency performance of your DAC.

I forgot to add a range check, but that's pretty easy:

Code: [Select]

integer_arr[np.where(integer_arr> HIGH)] = HIGH
integer_arr[np.where(integer_arr< LOW)] = LOW
where HIGH and LOW are the limits. This is another weird thing because ADCs don't accept negative values as far as I know, so typically I add 1 to the sine values to shift the range from (-1 to 1) to (0 to 2) and then scale by (2^bits)-1.

[BrianHG]

I forgot to add a range check, but that's pretty easy:

Code: [Select]

integer_arr[np.where(integer_arr> HIGH)] = HIGH
integer_arr[np.where(integer_arr< LOW)] = LOW
where HIGH and LOW are the limits. This is another weird thing because ADCs don't accept negative values as far as I know, so typically I add 1 to the sine values to shift the range from (-1 to 1) to (0 to 2) and then scale by (2^bits)-1.

Once again, such patching distorts the sine wave.
Do the all the math properly and you will properly hit your targets.

[OM222O]

Once again, such patching distorts the sine wave.
Do the all the math properly and you will properly hit your targets.

Code: [Select]

import numpy as np
idx = np.arange(17) # Number of samples per period
sf = idx.max() / (2*np.pi) # scaling factor for the period
arr = idx/sf # create a new array that goes from 0 to 2 pi in N steps
arr = np.sin(arr) # calculate the sin value for each point
integer_arr = np.round((arr*((2**13)-1))).astype('int32') # Scale the array by (2^13)-1 and then round the values(the actual sine values go between -1 and 1, giving you an effective range of 2, so you need to scale by max int/2)
print(integer_arr[:-1])
[    0  3135  5792  7567  8191  7567  5792  3135     0 -3135 -5792 -7567 -8191 -7567 -5792 -3135]

fun fact, removing the round produces EXACTLY what he initially posted, so I'm fairly sure that's how the table was made

[radiolistener]

I'm still not sure what the point of this topic is. There are an infinite number of phase shifts you can try and some may work better than others in specific test cases, but you always have some rounding errors.

The point of topic is how to generate sine wave for specific resolution (in my case 14 bit, 16 samples per period). To get as low as possible distortion/harmonics. I need it as a test vector. As you can see simple use of round or floor function doesn't provide best result.

If you want to minimize quantization error that's pretty easy to do mathematically. If you want to generate a specific frequency and phase shift, that's also pretty easy to do, but like others said, there is no "ideal sine wave".

Quantization error and phase shift doesn't matter for me. The goal is to get minimum possible sine distortion/harmonics level. I need a test vector for testing DSP block. DSP block works with much higher resolution than 14 bit of ADC source. I want to get maximum possible from 14 bit source.

Since I want to get ideal sine for specific conditions - 14-bit and 16 samples per period, ideal sample with sine definitely exists. Because one sample is better than other. So, some sample is the best. And I needs the way to calculate it.

You can re-write the program I gave you in any language and get the same results

I tried to use your program with online python compiler, include fix for sample length. But it produce dirty sine, I have no idea what is the reason for that.

but it seems pointless to worry about the harmonics noise as they can be filtered out in any good design. What's the main goal of generating the sine table?

No it cannot be filtered, I need a clean test vectors for testing DSP block. DSP block has 64-bit fixed point resolution and I want to see every small artifact which happens in signal processing. Such as spurs/harmonics.

The funny thing is that you don't even need a spectrum analyzer to test this, using any FFT analysis tool (numpy supports this) should give you the same results, so you can just simulate the whole thing and optimize it as much as you want, but again, I can't find a good reason for why you should.

Spectrum analyzer which I use is FFT based and is a part of software/gateware which I want to test with these test vectors

By the way, my FFT can have some errors, because I'm using some speed optimizations. I tested it and it seems that errors are below noticeable level, but who knows...

[radiolistener]

fun fact, removing the round produces EXACTLY what he initially posted, so I'm fairly sure that's how the table was made

No, just tested your code with removed round on online python compiller, the result is:

Code: [Select]

0  3134  5791  7567  8191  7567  5791  3134     0 -3134 -5791 -7567 -8191 -7567 -5791 -3134
But original sample has 5792 instead 5791

Here is original sample:

Code: [Select]

0 3134 5792 7567 8191 7567 5792 3134 0 -3134 -5792 -7567 -8191 -7567 -5792 -3134
Are you sure that your code produce the same?

[OM222O]

you're right, I missed the 1 difference since I was having a quick look, but for all intends and purposes that is HOW to generate a sine table. rounding, phase offset, scaling, etc. is the parameters you can play with if you want to optimize something