"Veritasium" (YT) - "The Big Misconception About Electricity" ?

[SiliconWizard]

Note that in real life, "DC" is more or less a fantasy. We're always dealing with time-varying fields. Even when the frequency is very low. (And anyway, you'll also have some high-frequency content - just with possibly very low amplitude, but not inexistent.) So in the end, it's always a matter of using an approximation that is "good enough" for a given application. There are always a ton of phenomenons that we are neglecting.

[SandyCox]

To get back to Veritasium’s problem: Under static (DC) conditions, there are both magnetic and electric fields in the empty space around the conductions. Together these give rise to a non-zero Poynting vector.
If there is indeed energy being transferred through this empty space, there is no way that it can be converted back to a useful form. For this we need a time-varying magnetic or electric field (or both). So, I choose to believe that there is no power transfer through empty space at DC.

Coming to think of it, the lightbulb requires a flow of charge (current) to heat up its element. Since the power travelling through empty space cannot be converted to a flow of charge, this cannot be the energy that powers the bulb. The energy has to come through the wires.

Since all the energy that leaves the battery is disspiated in the lightbuld there cannot be any energy transfer through open space at DC.

Maybe Dave should confront Veritasium with this argument.

[SandyCox]

Note that in real life, "DC" is more or less a fantasy. We're always dealing with time-varying fields. Even when the frequency is very low. (And anyway, you'll also have some high-frequency content - just with possibly very low amplitude, but not inexistent.) So in the end, it's always a matter of using an approximation that is "good enough" for a given application. There are always a ton of phenomenons that we are neglecting.

Very true, but lets break the bigger problem up into smaller subproblems and analyse one at a time.

[rfeecs]

By looking closely at Example 11.3.1 of Haus and Melcher we can see that Veritasium is wrong. In this example, all the power is being transferred by the conductors. No power is transferred in the region outside the conductors. Haus and Melcher should have said "power seems to flow through the open space" instead of "power is seen to flow through the open space".

The power entering the washer from the voltage source is:
Pw = 2*pi*sigma*delta*V*V/ln(a/b)
By integrating the Poynting vector over the outer surface, we find that the power that is dissipated in the washer is:
Pw = 2*pi*sigma*delta*V*V/ln(a/b)

The power entering the rod from the voltage source is:
Pr = pi*b^2*sigma*V^2/L
By integrating the Poynting vector over the outer surface, we find that the power that is dissipated in the rod is:
Pr = pi*b^2*sigma*V^2/L

So all the power entering the washer from the voltage source is dissipated in the washer and all the power entering the rod from the voltage source is disspiated in the rod.
There is no power being transferred in the region between the washer and the rod.

Will someone please check my calulations?

I checked.  Your calculations are wrong. 

You are missing the directions of the vectors.  For the rod, the S vector is radial, pointing in to the center axis.  So at the end of the rod, S is parallel to the surface.  S dot dA is zero at the end of the rod.  So the power entering the rod from the end contact is zero.  All the power is entering the rod from the region between washer and rod.

The same is true for the disk.

The power doesn't flow through the conductors, it flows in the space around the conductors.

The math still works.

[SandyCox]

By looking closely at Example 11.3.1 of Haus and Melcher we can see that Veritasium is wrong. In this example, all the power is being transferred by the conductors. No power is transferred in the region outside the conductors. Haus and Melcher should have said "power seems to flow through the open space" instead of "power is seen to flow through the open space".

The power entering the washer from the voltage source is:
Pw = 2*pi*sigma*delta*V*V/ln(a/b)
By integrating the Poynting vector over the outer surface, we find that the power that is dissipated in the washer is:
Pw = 2*pi*sigma*delta*V*V/ln(a/b)

The power entering the rod from the voltage source is:
Pr = pi*b^2*sigma*V^2/L
By integrating the Poynting vector over the outer surface, we find that the power that is dissipated in the rod is:
Pr = pi*b^2*sigma*V^2/L

So all the power entering the washer from the voltage source is dissipated in the washer and all the power entering the rod from the voltage source is disspiated in the rod.
There is no power being transferred in the region between the washer and the rod.

Will someone please check my calulations?

I checked.  Your calculations are wrong. 

You are missing the directions of the vectors.  For the rod, the S vector is radial, pointing in to the center axis.  So at the end of the rod, S is parallel to the surface.  S dot dA is zero at the end of the rod.  So the power entering the rod from the end contact is zero.  All the power is entering the rod from the region between washer and rod.

The same is true for the disk.

The power doesn't flow through the conductors, it flows in the space around the conductors.

The math still works.

I did take the direction of the vectors into account. So did Haus and Melcher when they calculated the integral of the Poynting vector over the outer surface of the rod and got the same answer as I did.

What you are doing is exactly the misinterpretation of the Poynting vector I am referring to.

You have to calculate the integral of the Poynting vector over the total outer surface of the rod. You then have to add up the contributions from the different surfaces before coming to a conclusion. You cannot conclude that Power is entering the rod through a particular surface by looking at the integral of the Poynting vector over that surface.

I suggest that you do the following:
Calculate the integral of sigma times E dot E o
ver the volume of the rod and the washer. This is the amount of electromagnetic power that is converted to heat (dissipated) in each of them. Now look at the problem from the circuit analyses point of view and calculate the current that is entering the rod and the washer. You will see that all the power that is transferred from the voltage source to the rod is dissipated in the rod. Likewise, all the power that is transferred from the voltage source to the washer is dissipated in the washer, i.e. there is no net transfer of power between the washer and the rod.

[rfeecs]

I did take the direction of the vectors into account. So did Haus and Melcher when they calculated the integral of the Poynting vector over the outer surface of the rod and got the same answer as I did.

What you are doing is exactly the misinterpretation of the Poynting vector I am referring to.

You have to calculate the integral of the Poynting vector over the total outer surface of the rod. You then have to add up the contributions from the different surfaces before coming to a conclusion. You cannot conclude that Power is entering the rod through a particular surface by looking at the integral of the Poynting vector over that surface.

OK, then I don't understand your point.  I thought you were saying there was some problem with the math of the Poynting theory.  Now you seem to be saying that the Poynting theorem gives the same result as P=IV.  That is no surprise and there is nothing inconsistent.

I suggest that you do the following:
Calculate the integral of sigma times E dot E o
ver the volume of the rod and the washer. This is the amount of electromagnetic power that is converted to heat (dissipated) in each of them. Now look at the problem from the circuit analyses point of view and calculate the current that is entering the rod and the washer. You will see that all the power that is transferred from the voltage source to the rod is dissipated in the rod. Likewise, all the power that is transferred from the voltage source to the washer is dissipated in the washer, i.e. there is no net transfer of power between the washer and the rod.

Again, you are saying P=IV.  So what?

Apparently you are concerned that the picture of the Poynting vector pointing from the disk to the rod doesn't seem to make sense.  This is similar to the circuit with three resistors discussed previously.  It looks like power is flowing from one resistor to the other.

So an explanation would be that power flows out of the power supply, to the space on the left of the disk, then all the power flows into the disk, some of that power is dissipated, the rest flows to the rod through the space between the disk and the rod, and that power is dissipated in the rod.

It's not a pretty picture?  But it can still account for what is happening and satisfy energy conservation.  As you say, just integrate over the closed surfaces and both conservation theorems still work at DC.

[Sredni]

Ascribing meaning to the Poynting vector at a point leads us to the wrong conclusion, as shown by Fig. 11.3.1.

I didn't see Haus and Melcher recant what they wrote

"Even with the fields perfectly stationary in time, the power is seen to flow through the open space to be absorbed in the volume where the dissipation takes place."

Did you?

I’m not quite sure what you a trying to say by “glowing red hot”. Are you saying that energy is now transferred through thermal radiation?

No, I'm saying that by making rod and washer of very different materials you can have one glow red hot while the other stays cool, and viceversa. There still will be Poynting field lines in the space inside the can and they will account for the difference between the total power delivered by the battery and the power absorbed by the rod.
In one case you will see a lot of lines coming out of a cool washer to impinge into a red hot rod.

On the next page they say:
" we illustrate the danger of ascribing meaning to S evaluated at a point, rather than integrated over a closed surface."

I'm not sure why you are dragging thermal issues into the argument. We can also make your resistors glow, but why would we? Add a cooling system if you are worried about conductors glowing red.

The point is that there is no power being transferred from the washer to the rod. All the power is accounted for. Misinterpreting the meaning of the Poynting vector leads us to incorrectly believe that power is flowing from the washer to the rod. Please do the calculations. You have all the information you require.

I used the cool washer and hot rod as an as an example of how counterintuitive it would seem to see power flow from a cool object to a hot one. And to highlight that the energy would not come from the cool washer, but from the battery.
Anyway, what follows was written a day or two ago. I had to draw and scan a few pictures and that took time, so some points might already have been discussed.

1) It is undeniable that there are both an electric field and a magnetic field in the space between (and more generally around) the wires. One can measure them.
But most importantly, one can use those fields to do work. Can we say that we are extracting energy from the fields?
I can use the E field to make an electric dipole rotate, for example. Or to slow down dust particles in the space near the wires and make them pile up. I can also use the B field to make a magnetic dipole rotate, like a compass needle in the space near the wires.
It takes energy to make that mechanical energy appear.


2) Where does that energy come from? It is said it comes from the fields.
Granted, the fields in the static case are not linked to one another as the E and B field of an EM wave (more on this in point 5 ), but they are still both generated by charges in your circuit.

     static charges:   surface charge on the conductors' surfaces and at the interfaces between materials
     moving charges: currents flowing in the conductors and displacement currents in dielectrics

the charges moving inside the conductor are the result of the field generated by the static charge on the surface, which in turn is distributed in that way because the battery has been connected to it.

Consider a charge magically materialized in the space between the wires of our circuit. The moment the electric field puts a charge in motion, a magnetic field appears, and the Poynting vector shows the charge 'stealing' energy from the field (changing it).If I put mechanical energy in to force a charge against 'its will' (for example to put it there from the 'chargeOort cloud' at infinity), I will end up adding energy to the field. Again, a Poynting vector field will appear to show energy getting into the field. If I move the charge back and forth slowly (quasistatically), I keep adding and subtracting energy to the field with no radiation.


3) Let's get to the Poynting vector at DC for the resistor alone. Oh, by the way, I hope it is clear that both rod and washers in that Haus & Melcher example are the resistors - the conductor is the cylindrical can.

For a homogeneously cylindrical resistor where a constant DC current is flowing the Poynting vector is directed radially in and decreases in magnitude to zero when it reaches the axis (because that's what the magnetic field magnitude inside does). Is energy disappearing from the universe? Of course not, it just gets converted into something else. The following figure shows the Poynting vector field for a resistor with a 5V potential difference across it:


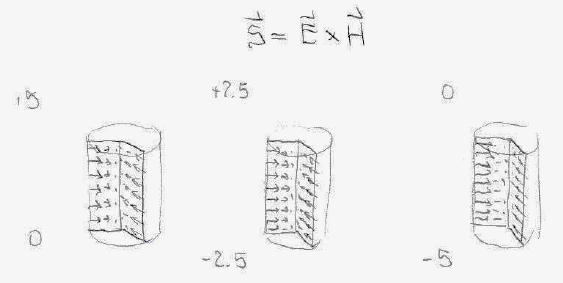fig Poynting for a cylindrical resistor - three cases

All textbooks dealing with energy balance by means of the Poynting field say we must always integrate over a closed surface, so all we can say is that, thanks to the distribution of surface charge on the circuit elements and the ensuing currents flowing, energy is getting into the resistor from outside.

You point out an alternative way to compute the power absorbed by the resistor that does not need to consider the electric and magnetic fields in the space around the conductor and circuital elements. Fine, instead of considering the whole of B you just take j into account. By resorting to the non uniquely defined potential function phi (with that arbitrary additive constant...) this method leads to an infinity of different configurations of energy flows. Same resistor with 5V potential difference, but different choice of the zero potential reference.



fig alternative Poynting for a cylindrical resistor - three cases

Luckily we must only consider the results of integration over a closed surface, still, the phi J representation appears to be weaker than the ExH representation.
Adding to the 'potential' nonuniqueness problem (which, one might argue, affects the ExH representation as well since we can still add an arbitrary zero-divergence vector to ExH), this alternative method is not a general method that takes into consideration the whole physical system. In fact, it does not take into account what happens in the space around the conductors and elements. It ignores the surface charges that give rise to the field inside the conductor, and only considers what happens where the current is flowing. In fact, it's blind in the space between conductors.


4)  You say that in Haus and Melcher's example, all energy is accounted for and therefore there is no need to have any transfer between washer and rod. But this is also true in the orange parallel resistors circuit: there is no energy transfer between the first resistor and the second one. In fact the first resistor takes in a net power equal to the power it dissipated in heat via Joule heating. (side note: The first resistor just happens to be in the way of the power transfer from battery to the rest of the circuit. It is not completely useless, though, because its surface charge and the current flowing in it helps in shaping the electric and magnetic fields that will affect the rest of the circuit.)

Moreover what about the perfectly conducting tin can in Haus & Melcher's example? Isn't it connecting the top of the rod with the outer perimeter of the washer? Is there a current flowing there? Is there any power flowing in there? From rod to washer? Let's unfold the geometry, and see what happens when the zero potential reference is placed somewhere else:


fig nut-washer circuit currents and equivalent circuit

So, is energy flowing through the conductor? Using the phi J representation it looks like the answer depends on where you set the zero for the potential:


fig nutwasher for three cases

We can see the inconsistencies of this representation of power flow by considering a single resistor with one side directly attached to the battery


fig one resistor two positions -
power flows in the conductor only if the battery is before the resistor?

what does these say about the way power go from the battery to the resistor? In one case the conductor is bringing power, in the other is does not? And if we add a conductor on the other side as well, one conductor is bringing power to the resistor and the other one doesn't? Does it reverse if we reverse the polarity?


fig one resistor two polarities - power flow alternates between the top and bottom conductors?

And if we call the battery terminals +V/2 and -V/2, power flows into the load from both conductors?
This representation of energy flow is as undetermined as the value of potential.

5)  Are all representations doomed to fail? Possibly. After all, every author warns the reader about only considering the results of the integration over closed surfaces. But we know that in the case of antennas, the energy does flow into space. Where does it stop to be in the space between conductors and starts hiding inside conductors (if ever)? When dE/dt becomes significant? What exactly makes the energy hide into the conductors?

Let's start with an EM beam at very high frequency, such as a laser beam. Is the energy in the space occupied by the beam? I guess it is. Let's lower the frequency and consider an RF antenna beam: is the energy in the space? I guess it still is.


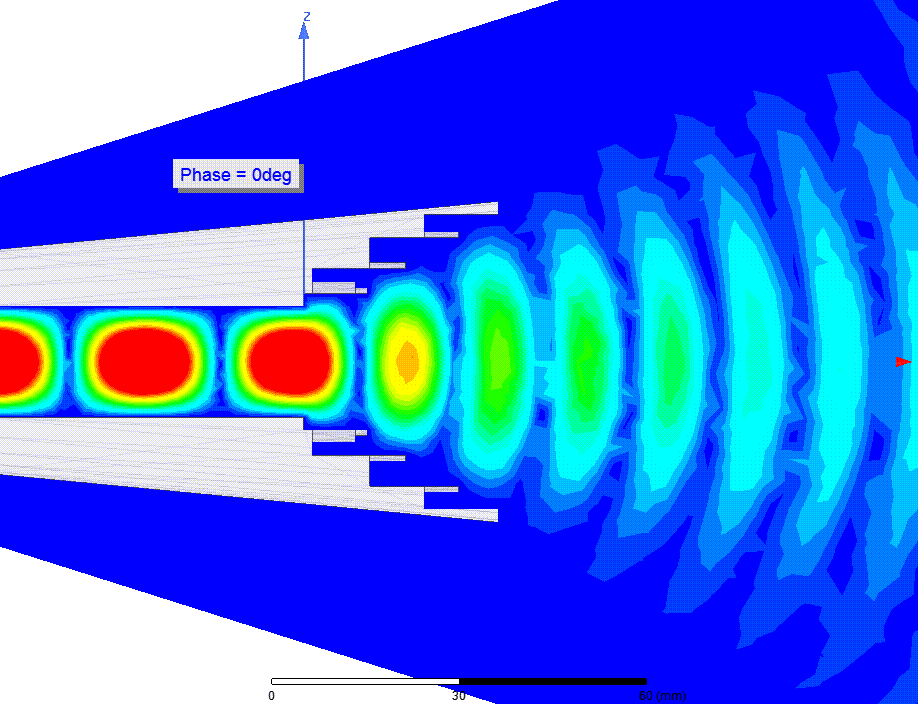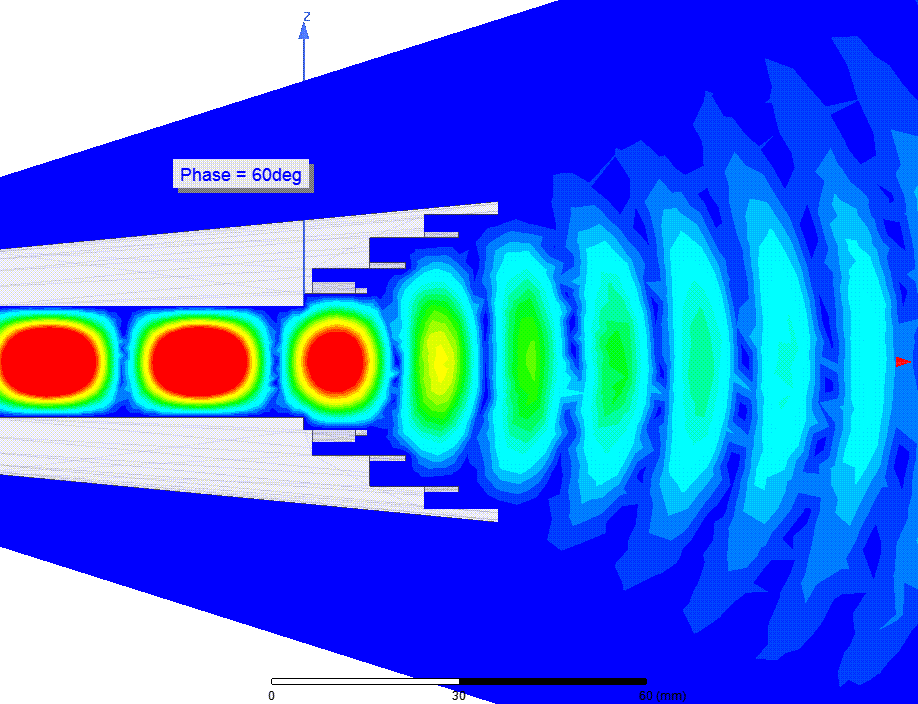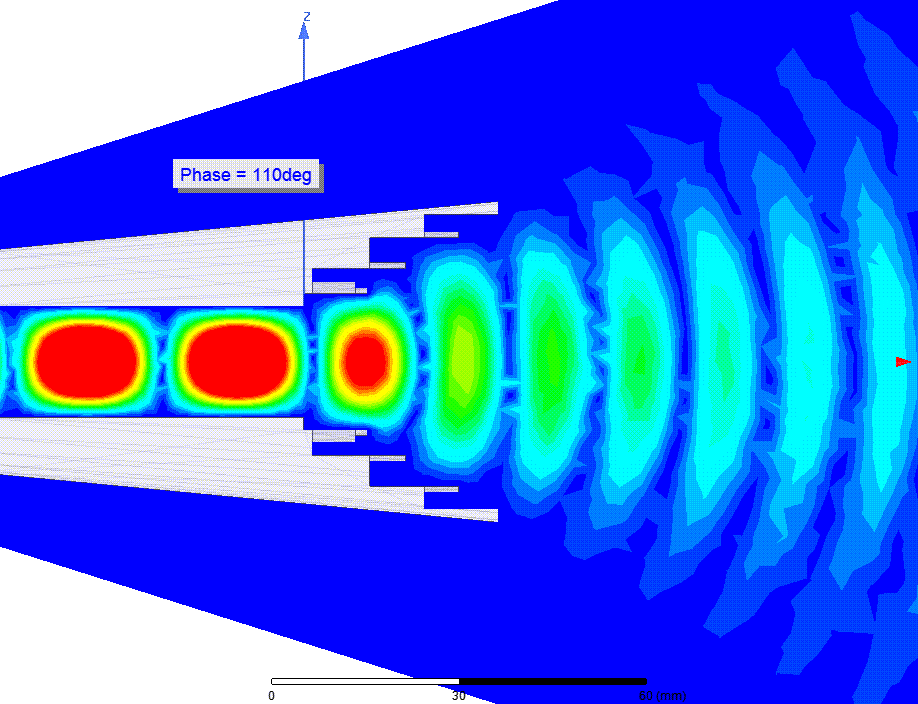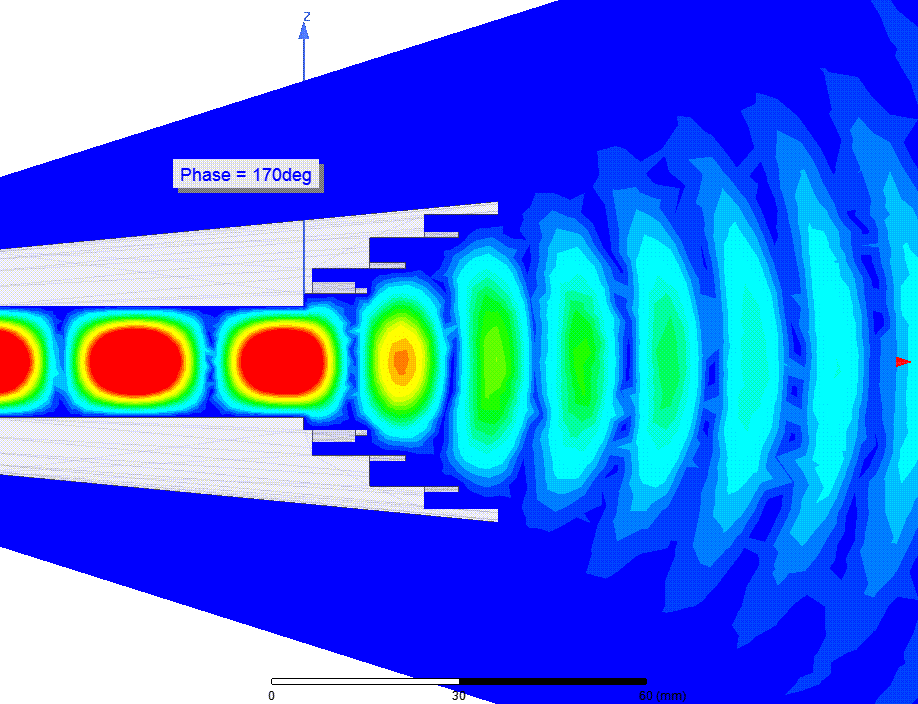fig antenna beam animation in space
source: sudonull

Lower it a little more and look at a transmission line feeding an antenna. I will add a resistor to steal some of the energy. Is there energy present in the space occupied by a beam exiting an antenna? If the answer to that question is yes, I would say that there must also be energy in the space between the conductors of the transmission line feeding the antenna.


fig animation from transmission line to free space

Now, keep lowering the frequency. The fields of a single 'cell' are basically following the same configuration, but the 'cells' gets longer and longer.




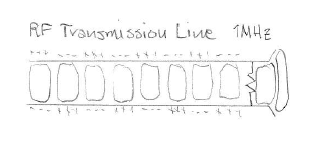
fig lowering the frequency

We will eventually get to a point where we no longer have appreciable radiation and the pattern gets stationary. Is the energy still in the space between wires as the frequency gets lower and lower?


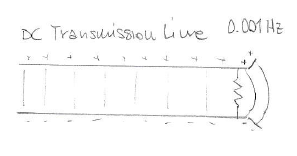fig transmission line from LF to DC - no radiation, just a fringe effect

When does the energy cease to be in the space between the conductors? At 1Hz? At 0.01 Hz? And at 0.00001 Hz? At DC (meaning from bigbang to bigcrunch)?

6)  Does the Poynting vector have a meaning when we do not have waves?
When Panofsky and Phillips, a book I respect and revere, consider the energy balance in the quasi-static case, they neglect the contribute of the ExH term because, they say, it goes to zero at least as 1/r^5.
But (and this is my thought) this dependency - which is true in the quasistatic state -  is relevant when... r is big. Near the sources, near the wires, with all their surface charge and conduction currents, ExH is usually not negligible. Case in point, in a long cylindrical circuit the magnetic field is approximately constant inside the cylinder, so ExH goes approx as E.
If we enclose our circuit in a bubble and look at the bubble from far away, yes, we will not see any EM energy coming out of our bubble - no diverging contribute of ExH, so to speak. But this does not imply there is no ExH transfer of energy in the circuit's guts.


Appendix
A philosopher might argue that the energy is in the charge and current distribution, and not in the space around them. Maybe, but if I have a ton of water at 0 meters altitude on an iron plated planet and no showel, I can hardly say that my water has any usable energy. But if my ton of water sits in a reservoir h meters above the surface, then there's energy. But is it in the water? Or is it in the gravitational field in the space between water and surface? I would say it is in the field of the composite system planet+water, but that's just me.

Note: a discussion of the engineer's perspective on the 'reality' or not of where the energy flows can be found in

    Edward G. Jordan, Keith J. Balmain
    Electromagnetic Waves and Radiating Systems 2e
    1968, Prentice Hall
    p. 169, section 6.02 "Note on the interpretation of ExH"

As a final side note: electric charges add a twist because they carry a significant field with them (much more than a mass particle - due to the difference in strength between gravitational and EM interaction one would need a reservoir the size of a moon to change the gravitational profile at the Earth surface).

Edit: fixed figure positions, specified position of charge between wires, clarified where Panofsky and Phillips consideration ended. Added philosophical appendix

[adx]

Note that in real life, "DC" is more or less a fantasy. We're always dealing with time-varying fields. Even when the frequency is very low. (And anyway, you'll also have some high-frequency content - just with possibly very low amplitude, but not inexistent.) So in the end, it's always a matter of using an approximation that is "good enough" for a given application. There are always a ton of phenomenons that we are neglecting.

That was going to be another idea, but the one I posed (oops Freudian for posted) above seemed much better.

I was wondering about the 0.001Hz idea which Sredni has since posted on (with the ExH insight), but I didn't expect anything very interesting to happen down there beyond the fields seeming to 'freeze' at DC. The way people in physics (from some recent reading) tend to deal with DC is kind of a linguistic limit approach applied to experimental reality (even of a numerical investigation), I forget the wording, but something like "as the system stabilises, the result is shown to approach the expected steady state...". They never say it actually is DC if something like this comes up (or just ignore it and assume DC if it doesn't). And things like bandlimiting out noise. I am guessing it is reasonable to assume that RF effects at ULF are negligible compared to at DC, but I don't have the insight of watching the fields and terms sweep 'down to' zero frequency.

So I was also / more wondering about the kind of thing I was going on about at:

But I have to concede that for the electrical system you [bdunham7] describe, energy does have to be put into those field(s) to make it work, so the DC analysis is a kind of fallacy (in that there is always going to be stored energy which is there and can conceptually be taken from, and refuelled at the other end). This is central to my gripe with Bernoulli's principle and its (I say false) assumption of conservation of energy. The system has to be charged up before it will work, and energy is different for different arrangements. ...

Well, that explains it. If the DCs / steady states are different (say for a circuit with the wires 1m then 0.5m apart) - same current, but different history and energy stored in that current from equilibrium (0), then perhaps something in the way the fields are set up then torn down before and after a 'rest' at DC, can help explain the Poynting vector? As something to look at rather than analyse mathematically (eg feeding it with a Tukey window shaped current pulse (cosine with flat top inserted at the top) to watch perhaps the fields settle in between cosine pieces into a kind of holding pattern amidst something that looks like RF).

Long shot.

[adx]

...
Coming to think of it, the lightbulb requires a flow of charge (current) to heat up its element. Since the power travelling through empty space cannot be converted to a flow of charge, this cannot be the energy that powers the bulb. The energy has to come through the wires.

Since all the energy that leaves the battery is disspiated in the lightbuld there cannot be any energy transfer through open space at DC.

Maybe Dave should confront Veritasium with this argument.

I like that argument, but Sredni and I have now suggested / shown that energy is continually being put into and taken from the field in a DC circuit. There is a superposition of time-varying situations going on.

I'd tend to frame it more like; the flow of charge that does the work on the filament is continuous in quantity all the way along the wires, so it can be argued that it is the source of the current (obviously) or magnetic field, and electric field along the distance of the wires (which is extremely low or even 0 in places, but balances itself over the length of the circuit). From force times speed, or voltage times current (same thing, physically), power is carried by the moving charges.

Sounds completely contradictory, but both are true as far as I can see, so it's more for looking for that elusive answer to the Poynting vector at DC. By that I mean the perfection with which the Poynting vector incorporates the magnetic field, to arrive at its bizarre looking but correct result. But I don't use "bizare" idly, it is because it is inexplicable and unproven at any stage in human history, afaik.

Ok, got to do for the night. Wrong timezone / virtual jetlag.

[SandyCox]

Thanks’ to Sredni for the detailed explanation. I need some time to draft a proper response.
For now, I would like to point out that the rotating electric and magnetic dipoles do not represent static conditions. The static fields may exert a force on the dipoles. There is no work being done if there is force without motion. As soon as they start rotating the time derivates of the magnetic and/or electric fields are no longer zero.

[Sredni]

For now, I would like to point out that the rotating electric and magnetic dipoles do not represent static conditions. The static fields may exert a force on the dipoles. There is no work being done if there is force without motion. As soon as they start rotating the time derivates of the magnetic and/or electric fields are no longer zero.

Yes. You put energy in the field when you push a positive charge in space towards the positive wire. The Poynting vector will appear briefly during the (ideally quasi-static) movement and will disappear when you are in the new steady-state condition. Where did the energy you put into pushing the charge go? In the system (comprising the charge).
Now, if you let the charge go by itself it will accelerate, so let's attach it to a damper in order to make it move (pushed by the field) slowly away from the positive wire. Poynting vector will appear again, showing energy going out of the system. Where did it go? Into the mechanical system (EDIT: yes it will eventually be dissipated as heat in the damper) necessary to assure the charge did not significantly accelerate.

If you let the charge accelerate, it will radiate and I expect the Poynting vectors to show energy leaving the system in the form of EM radiation.

If I wiggle the charge slowly enough not to have appreciable acceleration, I will see energy getting in and out of the system during movement - ideally I will balance to zero (EDIT: but no, the damper will take energy out by dissipating it, we need a magical quasi-static movement over an infinite time). If I wiggle it fast enough, in addition to energy going in and out of the system I will find that some energy is permanently leaving the system. I will not balance to zero for the system alone, because of radiation.

I would love to see an animation showing the Poynting vector field (and its time average) when a charge is wiggling from very slowly to very fast.

EDIT: I had forgotten that the damper would take energy out of the system. To make the addition and subtraction of energy reversible we need veeeeeeeeery slow motion.

[SandyCox]

For now, I would like to point out that the rotating electric and magnetic dipoles do not represent static conditions. The static fields may exert a force on the dipoles. There is no work being done if there is force without motion. As soon as they start rotating the time derivates of the magnetic and/or electric fields are no longer zero.

The Poynting vector will appear briefly during the (ideally quasi-static) movement and will disappear when you are in the new steady-state condition.

This implies time varying electric and/or magnetic fields. This not a static system.

The conundrum with the non-unique definition of the voltage is only a problem when we try to calculate the power that is transferred through a single wire. We always have to think of two wires, the current and its return path.

We know that electromagnetic energy can be transferred in a quasistatic system. The capacitor and transformer are examples. However, none of them will work in a static system.

The question is if electromagnetic energy can be transferred in a purely static system by means other than the flow of charge?

Here are two questions to which I do not yet know the answers:
1.   Will a fluorescent lightbulb glow in a static electric field? Is the field still static once it starts glowing?
2.   Is the following problem static: Chapter 7.5.2 (demo only): Rotation of an Insulating Rod in a Steady Current - YouTube

[SandyCox]

EDIT: I had forgotten that the damper would take energy out of the system. To make the addition and subtraction of energy reversible we need veeeeeeeeery slow motion.

Unfortunately this a not allowed. We are looking at the problem from the static point of view. We can split the solution to Maxwell's equations into static and transient solutions. We are only looking at the static solution.

[Sredni]

For now, I would like to point out that the rotating electric and magnetic dipoles do not represent static conditions. The static fields may exert a force on the dipoles. There is no work being done if there is force without motion. As soon as they start rotating the time derivates of the magnetic and/or electric fields are no longer zero.

The Poynting vector will appear briefly during the (ideally quasi-static) movement and will disappear when you are in the new steady-state condition.

This implies time varying electric and/or magnetic fields. This not a static system.

How do you expect to put or extract energy from an EM system if you do not allow for charges to change position (and moving when doing so)?
The circuit with a current flowing is not a static system. It has charges moving. It's quasi-static.

We know that electromagnetic energy can be transferred in a quasistatic system. The capacitor and transformer are examples. However, none of them will work in a static system.

Not even a resistor will 'work' in a static system. DC current is quasistatics. Charges are moving. They are not static.
What can be considered static is the pattern of the Poynting vector field, that will show energy coming out of the battery and getting into the resistor, to be converted to thermal energy.

Instead of having a single charge losing energy to a miniature damper, I have all the charges moving in the wire losing energy to the lattice inside the resistor (in the classical view).
If you want to see what happens in static conditions, wait till the battery is depleted.

(and no, subtracting the Poynting vector from itself won't help)

[snarkysparky]

charges moving along at the same rate produce constant fields.  So yes the charges are moving the  fields involved are constants. 

So the partial derivatives wrt time can be zeroed.

[SandyCox]

How do you expect to put or extract energy from an EM system if you do not allow for charges to change position (and moving when doing so)?

Exactly the point I am trying to make. How do we do it? How does the lightbulb harvest energy from the static electric and magnetic fields around it?

The circuit with a current flowing is not a static system. It has charges moving. It's quasi-static.

The electric and magnetic fields are constant over time. So it's a static system. Charge may move at a constant rate in a static system.


And we cannot add any solenoidal field to the Poynting vector. It violates the conservation of angular momentum.

[SandyCox]

If anyone knows of a way to harvest energy from the electric and magnetic fields near a High Voltage DC (HVDC) powerline, then get to your local patent office as fast as you can. You will become very rich.

[adx]

... still, the phi J representation appears to be weaker than the ExH representation. ... this alternative method is not a general method that takes into consideration the whole physical system. In fact, it does not take into account what happens in the space around the conductors and elements. ...

It shouldn't - that space serves no purpose and is provably irrelevant to the (quasi)static case.

4)  ... one conductor is bringing power to the resistor and the other one doesn't? Does it reverse if we reverse the polarity?

Obvious perhaps, but the Poynting vector evades that inconvenience by having power flow though an area it can't possibly get to - literally avoiding getting caught out by cutting through the fields and avoiding roads. Phi j makes sense if one considers that the flux of power represents the potential energy with respect to a known reference. So the fact that the 'power field' contains a constant flux at the extremes of voltage isn't any surprise when an integral of a closed surface needs to be used to arrive at the differential (or difference, change of power flux is where the energy goes).

Weak argument, but at least it has one.

5)... What exactly makes the energy hide into the conductors?

Quite possibly the fact it isn't all in the conductors - what's left goes in the conductors. The energy in flowing current is mostly outside the wire, the energy due to the electric field between the wires is there. But the energy transferring by the current and externally applied electric field has little to do with the internal energy (in the sense of 1/2LI^2 and 1/2CV^2). So non-internal energy could be considered to be hidden in the wires, with radiation coming as an external term or from the DC energy. Which is where my argument above comes in - a DC system cannot transfer power unless it is charged with current and voltage energy. No one doubts that is in the field(s). All doubt is over the energy conducted through an area. Even the concept of "energy flux" is odd; a flux of charge is stationary, a flux of charges physically moves. Is it possible to have energy transfer over such an area without something physical moving?

Let's start with an EM beam at very high frequency, such as a laser beam. Is the energy in the space occupied by the beam? I guess it is. Let's lower the frequency and consider an RF antenna beam: is the energy in the space? I guess it still is.

Not necessarily. In the feed, there is current in the walls. Without this it couldn't be constrained not to flow in random directions.

As the frequency lowers, there is undoubtedly potential energy in the voltage antinodes. That is where the current is the highest. So that is where the energy resides. Each cell is like a battery zipping along; E-field moving along with flow of charge (or opposite charge moving in a return path). (I am not suggesting the electrons are moving at the speed of light however, just the current.)

So the "error" my head created must not be real and the answer correct: DC is a travelling wave propagating at the speed of light locked at phase 0. The fields don't "freeze", there is nothing in the progression of lowering frequency that suggests the speed is in any way reducing - even when the size of a cell (half wave) runs well over the edge of the screen. There is always something just out of view that could potentially zip through, and that will be at the speed of light. You just can't see it until it happens, providing an illusion of steady state.

It therefore follows that the energy continues to flow at the speed of light, exactly as the RF behaviours suggest (yes, Maxwell and Poynting). There we have exactly the same problem with current, whether it be in wires or walls of the waveguide (or that copper block I cut through with the rubidium laser): It exists if the wave is not to be free. Charges move longitudinally, and are worked on and do work, and move in chains which are absolutely required to conduct the field to a distant source as the frequency gets too low to focus effectively. If that needs to be thought of in terms of magnetic field (technically correct because the effect travels at the speed of light and is a force) then so be it, but ultimately it is a string of balls being pushed along by a force. It depends on what your personal view of current is.

[Sredni]

Exactly the point I am trying to make. How do we do it? How does the lightbulb harvest energy from the static electric and magnetic fields around it?

Those fields are what cause the surface charge distribution that will have current flow into the resistor.

The electric and magnetic fields are constant over time. So it's a static system. Charge may move at a constant rate in a static system.

I agree that I shouldn't have used 'quasi-static' for this steady-state electrodynamic system. I have already written a longer answer to explain what I meant and how you can get energy in and out of the system at constant velocity. I need to fetch a quotation from a book, but I don't remember which book it was so I will post it later.

And we cannot add any solenoidal field to the Poynting vector. It violates the conservation of angular momentum.

Here I was answering to the post you deleted. The one about subtracting ExH to himself to prove there is zero energy flow. Was it someone else, or I just imagined/misconstrue what you wrote in it?

If anyone knows of a way to harvest energy from the electric and magnetic fields near a High Voltage DC (HVDC) powerline, then get to your local patent office as fast as you can. You will become very rich.

Or very jailed. I will not mention current transformers, too easy.
Here's another method: attach a capacitor to the line and draw your power.
Oh, energy flows in the conductor joining the powerline to the capacitor? Let's remove that part. Upper armature is the cable, lower armature a metallic plate placed under the cable, let's say half a meter (less? Do you like sparks?) and attached to a metal pole. If no power will flow, then you can do this experiment safely keeping the metallic pole in your hands with your naked feet on the moist ground below.

Make sure you bring someone with you when you do the experiment.
Possibly with a broom and an urn.

Of course, DC not AC - silly me.
Ok, I can take a bit of energy out from that as well. It's in the answer I have written but I am using the charge near the resistor to make a charge in space move.

[rfeecs]

Will a fluorescent lightbulb glow in a static electric field?

Yes:



But would it work in a vacuum?  Probably not.

The way to get the bulb to light up is simple.  Connect it with wires.  The Poynting theorem still holds.

[Uttamattamakin]

I like your video very much, especially that part where you say that, in QFT, there's no distinction between particles and fields. But I have a question. What if your wire, besides the interacting electrons you showed, also had protons?

Taking account of the protons in the wire would make the model harder to work out and add a correction to the math but it would not change the fundamental semi-classical result.  That the probability of one field interacting with the other would be approximated by the inverse square law.  With a much greater probability of interaction the closer they are (at inter atomic distances) than at a meter apart. 

Treating the wire as a sea of free electrons loosely bound to essentially stationary atoms is the standard way that physicists handel conductors or semi conductors.  This works for a lot of reasons.  Assuming that the energy applied and the temperatrues achieved are not enough to rip apart the atoms the protons should not move much at all.  At most they'd vibrate around equilibrium a little bit and that would introduce a small perturbation to the calculation. 

In short outside of a proton accelerator we don't have to worry about a current of protons.

Now in a semi conductor there can be a current of positively charged holes. Absences of electrons which move like electrons inside the semi conductor. Then there are high energy physics experiments involving positrons ...   As you can see things go way beyond the scope of this problem.  For the purpose of this problem one can ignore the protons.

Cool, so the energy-carrying particles are the photons, which are just oscillations in the EM field.

In the QFT way of thinking about this there is no larger EM field.  What we measure as an EM fields are just coherent states of large numbers of photons.  The fields in Quantum Electro Dynamics are the electron (and it's anti particle) and the photon (which is its own anti particle).  When the right limits are taken we recover the classical description

I am not talking about the measurements, they will be as they always have been. I'm talking about the the title of this thread "The Big Misconception About Electricity". Does the energy flow in the field around the wire or does it flow in the wire at DC? Poynting/classical field theory says outside, QFT appears to say inside.
I want to know what you and others who have been so (not incorrectly) dogged about anyone that dares think of this in any other way than Maxwell/Poynting think about this apparent conundrum.

What I'm saying is that I am not at all sure that the QFT theory pointo of view is at odds with what is forecasted by Poynting. It might make it harder to see, but if you get the same measurements for the fields, then chances are that energy flow will follow what Poynting forecasts.

Regarding that video on QFT, it seems to me the point made is that the conductors are best at 'communicating' the electric field. And I can see that in classical theory as well: if there is only the battery, the electric field of each pole dies off as 1/r^2, and whatever field was there near the poles of your 12V battery, will be greatly attenuated at the distance of 1 meter. But if you attach cables at the two poles and place the other ends near each other (let's say the same distance as the battery's electrodes) one meter away from the battery, you will basically see there the same field you see between the electrodes.
Now, if QFT explains this through probabilities of interactions, instead of fields propagating from charges, well, good for QFT. But does this tell us where the energy actually flows in the first few nanoseconds in Derek's experiment?
In a post above the author of the video says

It's not "at odds" with it.  All QFT predicts is that while energy can flow via the path Pyonting predicts it can also flow via an Infinite number of other paths.  Incuding paths via the wire.  When one carries out the computation, taking account the presence of existence of the wire as a path of charges which are very close toegher for the battery to interact with, the path of highest probability is along the wire.  The path suggested by Pyonting also exist but the probability of conduction via that path is low. 

The classical theory is not "wrong" it is just too limited for this situation.  The very size of it makes the speed of light relevant and so relativity has to be accounted for.

One could even leave out the QFT aspect of this and analyze the problem using classical relativistic E and M.  What does the E and M field Tensor do in this situation?  Does the Pyonting vector, a cross product, even still make sense in 4d Space time?  In that space time instead of a Pyonting vector we get the E and M stress energy tensor. The pyonting vector is just one part of that. 

Such is why I wanted to just skip all of those intermediate levels and go for the most fundamental theory we have that deals with electricity and magnetism.  The experiment carried out in one of the other videos (the one where someone actually really did the set up with 1 KM of wire) more or less proved it right.  You get a TINY current right away (because there is a low probability path for that energy to travel, predicted by QFT and compatible with the pyonting vector.  Then after the right amount of time passes the higher probaility path, via the wire, the path of least reisistance if you will, the energy arrives at the bulb.

It was a trip that for about two weeks if one googled "Veritasium is wrong" a quote from my blog was the snippet of text that Google put up there. Now that is POWER. 

IT felt like 
https://youtu.be/W8lr7II3dwQ?

[adx]

I know it's not, but this sounds very simple in its answer that energy flows mostly in the wires.

I think I see where this comes from now: Those of us in classical land have been struggling with what energy "is", arguing over what voltage and current is and how it translates into energy or power. But for QFT, energy is the fundamental quantity, so it's hard to argue against a statement that it flows via the path of least (mathematical) resistance. Very direct result.

I still have some internal concern that QED relativistic EM deals with potential energies (pressure) rather than real power flow, but that's probably not relevant to this discussion, and I don't even know where to begin on QFT itself.

If I want to go further I'm going to have to get my feet wet with the mathematics, which I never really liked the idea of. I'm fine with numerical simulation (in Excel - only joking, use BASIC  ).

[daqq]

COMSOL jumps into the fray:

https://www.comsol.com/blogs/how-long-does-it-take-an-engineer-to-turn-on-a-light-bulb/?utm_content=bufferc79f7&utm_medium=Social&utm_source=LinkedIn&utm_campaign=comsol_social_pages

Simulation video included.

[SandyCox]

Quote from: daqq on Today at 09:29:34 am

COMSOL jumps into the fray:

>https://www.comsol.com/blogs/how-long-does-it-take-an-engineer-to-turn-on-a-light-bulb/?utm_content=bufferc79f7&utm_medium=Social&utm_source=LinkedIn&utm_campaign=comsol_social_pages

Simulation video included.

The blue line is a comparison of COMSOL's result with transmission line theory.

Note that the blue line is not a simulation. It comes straight from the theory.
 comsol.png (21.94 kB. 974x493 - viewed 245 times.)

[Sredni]

Can you zoom in in the first ten nanoseconds, to see how well they match?