Boltzmann constant

[fonograph]

I am learning about Boltzmann constant and I find the describtion on wikipedia slighlty confusing and non-noob friendly.

Correct me if I am wrong : Boltzmann constant is average kinetic energy of a single particle inside gas of certain temperature.The particle here means either atom,like a noble gas/plasma or molecule like nitrogen/oxygen etc

[T3sl4co1l]

This is definitely not accurate language / terminology.  I don't know if that's because of language alone (I assume you're ESL) or misunderstanding the concept.

You seem to be on the right track, however it is not the "average kinetic energy of a single particle", but of each degree of freedom.  And, usually half, I think, but I don't remember why.

Degrees of freedom (axes) include: x/y/z velocity of ideal gas particles (giving rise to the 3/2 k_B * T term), rotational (theta, phi) modes of simple molecules (giving 5/2), and still more for more complex molecules.

And that's in molar terms, so there's a gas constant in there too, to get the volumetric or specific property.

Often, more degrees of freedom become available as temperature rises, hence C_p rises (usually somewhat in stages).  Example: vibrational modes are higher energy than rotational modes, so C_p rises as the energy spectrum spreads into that range.  (Meanwhile, low energy modes saturate and cannot hold additional heat; an example -- though probably not the best example, just one that comes to mind: nuclear spins in a solid, which have a very small energy difference under ambient magnetic fields, therefore the population holds nearly equal fractions in the parallel and antiparallel spin states.  Nuclear spin heat capacity is only relevant at very low temperatures and strong magnetic fields, where the populations have a significant gap.)

Tim

[fonograph]

Correct me if I am wrong : Single atom can have kinetic energy only in 3 degrees of freedom,X,Y,Z,the three dimensions of space but diatomic and polyatomic molecules can store kinetic energy in more ways than simply flying in certain direction in 3 dimensional space,they can also vibrate,rotate and spin.

Boltzmann constant is average kinetic energy of single particle in one of its degrees of freedom.

[T3sl4co1l]

Better to say: "The Boltzmann constant relates the temperature to the average kinetic energy in a degree of freedom."  The constant is, well, a constant, which wouldn't be very useful otherwise, and is not in units of energy anyway.

Tim

[fonograph]

So the Boltzmann constant is average energy per degree of freedom at certain temperature?

If yes,does that mean that single diatomic or polyatomic molecule holds more kinetic energy at certain temperature than single atom would? Becose single atom have only 3 degrees of freedom,but molecule can have like 5 or more so if one degree of freedom holds on average certain amount of energy,that mean single molecule would on average have more kinetic energy than single atom becose it have more degrees of freedom,is that correct?

Lets say at 300 Kelvin  1 degree of freedom  = 1 joule on average

Then helium atom  3 degrees of freedom  x 1 = 3

Oxygen  5 degree of freedom x 1 = 5

[T3sl4co1l]

Well, setting k_B = 1 doesn't get you kelvin or joules (one or the other, or both).  The proportions for molecules are correct.

Tim

[fonograph]

Wait,you mean I was right  with the idea that molecule have more kinetic energy than atom at same temperature?

[awallin]

If yes,does that mean that single diatomic or polyatomic molecule holds more kinetic energy at certain temperature than single atom would? Becose single atom have only 3 degrees of freedom,but molecule can have like 5 or more so if one degree of freedom holds on average certain amount of energy,that mean single molecule would on average have more kinetic energy than single atom becose it have more degrees of freedom,is that correct?

yes.
page 7, table 13-1 over here might be illuminating:
https://web.phys.ksu.edu/fascination/Chapter13.pdf

but it gets complicated... for some vibrational modes the energy required to excite them is so high it would require a very high temperature to excite them, see e.g. discussion here:
https://www.researchgate.net/post/Relationship_between_heat_capacity_and_molecular_structure_Who_could_help_me_explain_it

so you can't simply count degrees of freedom to derive a heat-capacity, you also need to consider the 'stiffness of the springs' for each mode.

[fonograph]

Thats some weird "strings" !  I guess these molecular strings work in way that unless you pass certain energy treshold they wont vibrate,so this vibrational degree of freedom cant hold energy unless it gets very hot,right?

Is this some kind of quantum phenomenon? Like electron orbitals that have fixed quantized levels?

[T3sl4co1l]

Yes. Most quantum states are evenly spaced, for example the energy levels of a "particle in a box" (i.e., the x-y-z momentum degrees of freedom)  are spaced quite closely in a macroscopic 'box', leading to a classical continuum: the ideal gas.

Rotation and vibration work similarly.

These states are derived using "ladder operators", so that you climb from one state to the next, with a given amount of energy (that's approximated as constant) per step.

This breaks down in certain limits, but is useful for a first-pass approximation.  Example: at high vibrational energy levels, the potential binding a molecule together, drops off.  This is a consequence of the potential being, not parabolic, but sharp on one side (atoms repel each other strongly as their inner orbitals are pushed together, generating additional force) and asymptotic on the other (the potential holding the atoms together is limited, and drops to zero at large distances).



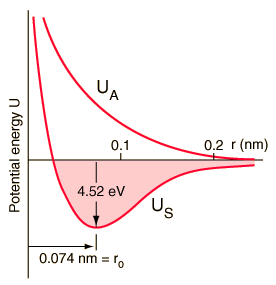
The potential well becomes wider and shallower towards the top, causing energy levels to be spaced more closely together; eventually the energy between levels is negligible, and the quantum number (corresponding to any given level) becomes hard to pin down -- because amounts of energy much greater than this are being tossed around.  The result is the atom slipping out of place from time to time: dissociation, giving rise to free radicals, or ions (depending on other properties of the atoms).

Dissociation and ionization is another degree of freedom, so the heat capacity goes up again around this range; this is the phase transition from gas to plasma.

At low temperatures, there isn't enough energy to climb the first one or few energy levels of vibration on average, so the heat capacity contribution is negligible.

For more complex molecules, with weaker bonds, this can occur at lower temperatures, and you get decomposition products: charring, combustion, destructive distillation, etc.  Which is of course very useful to the chemist, when it proceeds in an orderly manner.

Tim